9 图论：路径与圈

Definition(Graph 图)

$G = (V, E)$

1. V 是顶点的集合
2. $E \subseteq \{\{x, y\}\ |\ x, y \in V \land x \neq y\}$ 是边的集合

Definition(Walk 道路)

图 $G$ 中的(有限)道路是指像以下形式的一群边：

$\{v_0, v_1\},\{v_1, v_2\},\dots,\{v_{m-1}, v_m\} \\ (v_0 \to v_1 \to v_2 \to \dots \to v_m)$

是一条从起始顶点 $v_0$ 到终止顶点 $v_m$ 的道路

Definition(Trail(迹))

迹是一条没有重复的边的道路

Definition(Path(路径))

路径是一条没有重复顶点的迹

Definition(Cycle)

圈是封闭的路径，且至少有一条边

(封闭：$v_0 = v_m$)

Definition(正则图)

每个顶点的度数都相同的图叫做正则图，如果度数为k，那么叫做$k$-正则图。

Definition(欧拉迹)

只经过每条边一次而遍历图 $G$ 中的所有边

Theorem(欧拉迹)

如果一个图有欧拉迹 $\iff$ 只有两个顶点或没有顶点的度数是奇数。

Theorem(欧拉图)

一个连通图 $G$ 有欧拉圈 $\iff$ 所有顶点的度数都是偶数

这样的图叫做欧拉图

Definition(哈密尔顿路径)

只经过每个顶点一次而遍历图 $G$ 中的所有顶点

Definition(哈密尔顿圈)

哈密尔顿路径且是一个cycle，这样的图我们成为哈密尔顿图

Definition(Semi-Hamiltonian Graph)

有哈密尔顿路径而没有哈密尔顿cycle，称为半哈密尔顿图

Theorem(Example of Hamiltonian Graph)

1. 所有圈都是哈密尔顿图
2. 所有顶点数 $>$ 2 的完全图都是哈密尔顿图 ($K_3, K_5$)
3. 完全二部图 $K_{m,n}$ 是哈密尔顿图 $\iff$ $m = n \ge 2$
4. 所有正多面体变成图都是哈密尔顿图(4/6/8/12/20面体)
5. 皮特森图不是哈密尔顿图

Theorem(Ore’s Theorem)

图 $G$ 是顶点数 $n \ge$ 3 的简单图，如果

$deg(u) + deg(v) \ge n$

对于图 $G$ 中的任意一对不相邻的顶点 $u, v$ 都成立，那么图 $G$ 是哈密尔顿图(反过来不成立)

Method(图论的证明方法)

反正，通过找到某种情况的极大值(比如找到极大的某条路径)，来推出矛盾。

Theorem(Dirac’s Theorem)

简单图 $G = (V, E)$ 拥有 $n \ge 3$ 个顶点是哈密尔顿图 $\iff$

$\forall v \in V.deg(v) \ge \frac{n}{2}$

$\delta(G) = \min_{v \in V}deg(v) \qquad \Delta(G) = \max_{v \in V}deg(v)$

${\color{Red} \delta(G) \ge \frac{n}{2}}$

Definition(连通分支)

图的连通分支是在一个子图中，任意两个顶点都有一条路径相连，且不和剩余图中的其他顶点相连，连通分支的熟练记为 $c(G)$

Theorem

如果图 $G = (V, E)$ 是哈密尔顿图 $\Longrightarrow$

$\forall S \subset V.c(G - S) \le |S|$

Remark: 必要而不是充分条件，经常是反过来说明某个图不是哈密尔顿图。

---

10 图论：树

Definition(树、森林)

1. 树是一个无环的连通无向图。
2. 森林是多个树组成的图，每个树都是一个连通分支。

Definition(Leaf(叶子))

顶点数 $\ge 2$ 的树 $T$ 中，对顶点 $v$：

$deg(v) = 1$

那么 $v$ 是一个叶子节点，如果不是的话，$v$ 叫做内部节点

Lemma

所有的顶点数 $\ge 2$ 的树 $T$ 都包含 $\ge 2$ 的叶子，且 $\sum_{v \in V}deg(v) = 2n - 2$

Lemma

从有 $n$ 个顶点的树 $T$ 中删除一个叶子会产生顶点数为 $n - 1$ 的树 $T^{’}$

Theorem(Characterization of Trees)

$T$ 是一个无向图有 $n$ 个顶点，那么下述的所有公式是等价的

1. $T$ 是树
2. $T$ 是无环的，且有 $m = n - 1$ 条边
3. $T$ 是连通的，且有 $m = n - 1$ 条边
4. $T$ 是连通的，且每一条边都是桥(bridge)
5. 任意两个 $T$ 中的顶点都只被一条路径相连
6. $T$ 是无环的，但任意添加一条边都会多一个新的环

Definition(bridge)

图 $G$ 中的桥是一条边 $e$ 使得：

$c (G - e) > c(G)$

生成树

Definition(子图)

Definition(诱导子图)

由图 $G$ 顶点的一个子集和该图中两端的顶点均在该子集中的边的集合所组成的图

Definition(生成树)

无向图 $G$ 的生成树 $T$ 是一个包含 $G$ 中的所有顶点的树的子图。

Theorem

所有连通无向图中都有一个生成树(重复删除圈中的边直到图 $G$ 是无环的)

Definition(最小生成树MST)

图 $G$ 的边有权重(edge-weighted)，最小生成树是指权重最小的生成树

Theorem

所有有权重的连通无向图 $G$ 都有最小生成树

Algorithm(如何找到最小生成树)

1. 重复添加下一条权重最小的边，且不会生成环，直到 $n-1$ 条边被添加
2. 从已经构成的树开始重复添加与树相连且权重最小的边，直到 $n-1$ 条边被添加

Theorem(Cut Property)

${\color{Blue} X:}\ A\ \ part\ \ of\ \ some\ \ MST\ \ T\ \ of\ \ G \\ {\color{Blue} (S, V \setminus S):}\ A\ {\color{Red} cut}\ such\ taht\ X\ does\ not\ cross\ (S, V \setminus S) \\ {\color{Blue} e:}\ A\ lightest\ edge\ across\ (S, V \setminus S)$

Theorem(Cycle Property)

1. $C$ 是连通无向图 $G$ 中任意一个 $cycle$
2. $e = (u, v)$ 是 $C$ 中权重最大的一条边(有多条则随机选择一条)

那么 $\exists MST\ T\ of G:e \notin T$

Theorem(最小生成树的唯一性)

如果 $G$ 的每一条边权重都不相同，那么图 $G$ 只有唯一一个最小生成树(反之不一定成立)。

---

11 图论：平面图与图着色

Theorem(四色定理)

所有地图都可以只被四种颜色图画，且每两块相邻的地区颜色不同

所有地图都可以产生于一个平面图，顶点对应的就是不同的地区

Definition(k-Colorable(k-可着色的))

$G$ 是连通无向且没有自环的图，如果他的顶点可以用k种颜色画出，且相邻顶点的颜色不相同，那么称图 $G$ 是 $k$-可着色的。

Definition(k-Chromatic(k-色数的))

如果 $G$ 是 $k$-可着色的，但不是$(k-1)$-可着色的，那么 $G$ 是 $k$-色数的。

$\chi(G) = k$

Theorem(一些着色的例子)

1. $G$ 是 1-可着色的 $\iff$ $G$ 只有一个顶点
2. $G$ 是 2-可着色的 $\iff$ $G$ 是二部图
3. 皮特森图是 3-色数的
4. 所有简单平面图都是 4-可着色的

Theorem

$G$ 是简单连通图。那么，

$\chi(G) \le \Delta(G) + 1$

Theorem

$G$ 是简单连通图，且 $G$ 不是完全图或者有奇数长度的 $cycle$ 。那么，

$\chi(G) \le \Delta(G)$

Definition(平面图)

平面图是指可以在边没有交叉的情况下画在一个平面上的图。

所有平面图都可以将所有边以直线形式画出来。

Example:

1. 完全二部图 $K_{3,3}$ 不是平面图
2. 完全图 $K_5$ 不是平面图
3. 皮特森图不是平面图

Theorem(平面图的充要条件)

一个图是平面图 $\iff$ 这个图包含一个与 $K_5$ 或 $K_{3,3}$ 同态(homeomorphic)的子图.

Definition(同态(Homeomorphic))

两个图是同态的 $\rightarrow$ 一个图可以通过在另外一个图中，删除或者添加度数为2的顶点获得

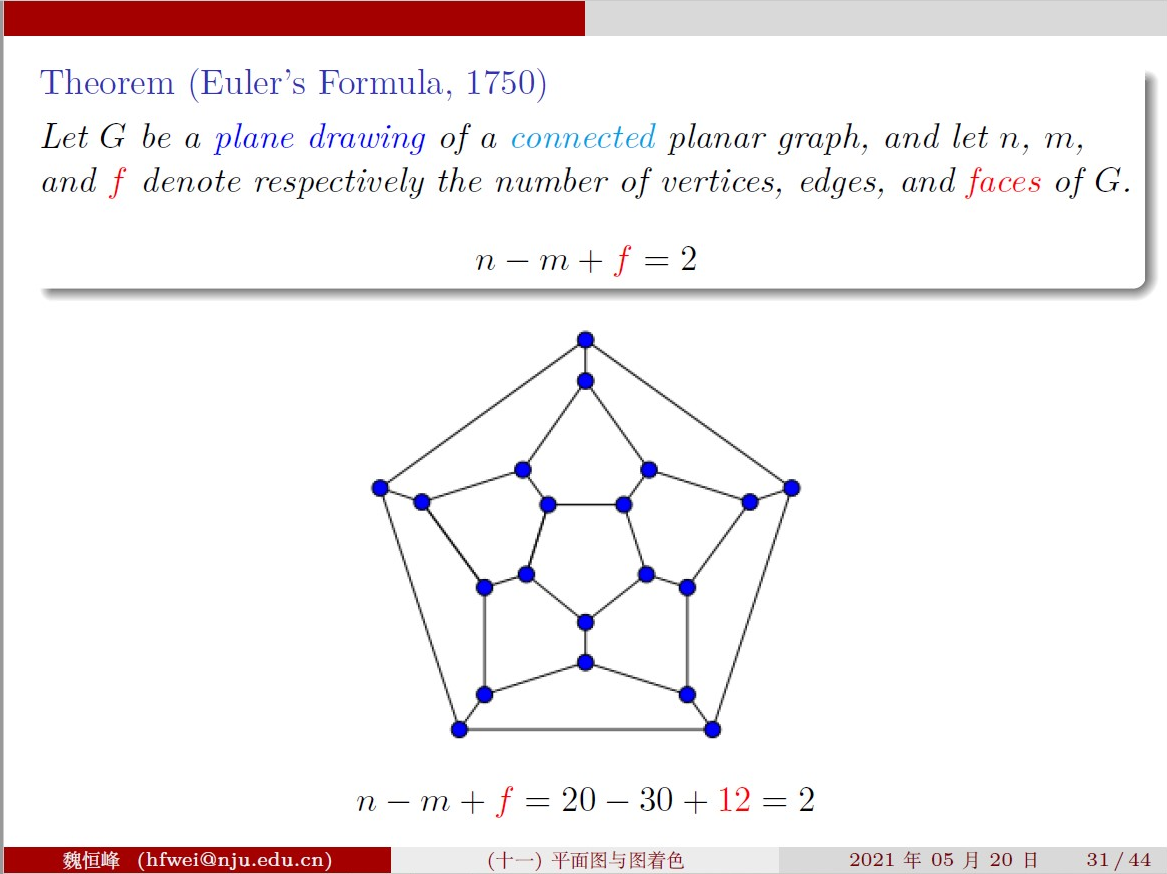
Theorem(欧拉公式)

图 $G$ 是一个连通的平面图，且已经按照没有交叉的画法画好，$n$: 顶点数量， $m$: 边的数量，$f$: 图 $G$ 的面(face)的数量，那么有：

$n - m + {\color{Red} f} = 2$

Remark： 外围也算一个面

Theorem

$G$ 是一个简单连通平面图且顶点数 $n \ge 3$，有着 $m$ 条边。那么

$m \le 3n - 6$

$3f \le 2m$ : 至少三个顶点才能构成一个面，且在计算面的时候每条边被用了两次。所以 $m \ge \frac{3f}{2}$

Theorem

$G$ 是一个简单连通平面图且顶点数 $n \ge 3$，有着 $m$ 条边，且 $G$ 中没有三角形。那么

$m \le 2n-4$

$4f \le 2m$: 没有三角形所以至少4个顶点才能构成一个面。

Theorem

所有简单平面图都有一个顶点的度数 $\le 5$

Theorem(六色定理)

Theorem(五色定理)

---

12 图论：匹配与网络流

匹配

Definition(Matching(匹配))

图 $G$ 中的匹配(matching)是指没有相同端点的边的集合。

即：集合中的每条边的两个端点都不相同

Definition(X-Perfect Matching)

$G = (X, Y, E)$ 是一个二部图，$X$ 完美匹配指的是覆盖所有 $X$ 中的顶点的匹配。

Theorem(Hall Theorem)

$G=(X,Y,E)$ 是二部图。$G$ 中有 $X$ 完美匹配 $\iff$

$\forall W \subseteq X.\big\vert W \big\vert \le \big\vert N_{G}(W)\big\vert$

Remark: $N_{G}(W)$ 代表的是 $W$ 中每个顶点 $x$ 所连接的 $y$ 的集合。

Definition($M$-alternating Paths)

$M$ 是一个匹配，$M$-alternating path 是将不在 $M$ 中的边替换成 $M$ 中的边构成新的路径

Definition($M$-增广路径)

$M$-增广路径是一条 $M$- alternating path 且这条路径的两端不在M中

此时就可以通过alternating来替换一个更大的匹配

Definition(点覆盖)

图 $G$ 的点覆盖是一个集合 $Q \subseteq V(G)$ ，且包含所有的边

即这个集合中的点所延伸出的边是包含图中所有的边

Theorem(弱对偶定理)

图 $G$ 中最大的匹配 $\le$ 图 $G$ 中最小的点覆盖

Theorem(König (1931), Egerváry (1931))

$G$ 是二部图。图 $G$ 中最大的匹配 $=$ 图 $G$ 中最小的点覆盖

网络流

Definition(网络)

网络是一个有向图，且

• 特殊的源点 $s$
• 特殊的汇点 $t$
• 每条边都有容量(capacity) $c(e) \ge 0$

Definition(流(Flow))

流 是一个赋予网络每条边值(value) $f(e)$的函数

Definition(可行流)

一个流是可行的当它满足：

1. $\forall e \in E. 0 \le f(e) \le c(e)$
2. $\forall v \in V.f^+(v) = f^-(v)$

Definition(值value)

流 $f$ 的值 $val(f)$ 是

$val(f) = f^-(t) = f^+(s)$

Definition(最大流)

最大流是拥有最大值的可行流

Definition(f-augmenting Paths(增广路径))

当 $f$ 是可行流时，一个$f$-增广路径是在底图(underlying graph)中的一条从 $s$ 到 $t$ 的路径 $P$ 且满足对每一条边 $e \in E(P)$

• 如果 $P$ 是朝前的，那么 $f(e) < c(e)$
• 如果 $P$ 是朝后的，那么 $f(e) > 0$

$\epsilon(e) = \left\{\begin{matrix} c(e) - f(e) \qquad e 在 P 中是朝前的 \\ f(e) \qquad e在P中是朝后的 \end{matrix}\right.$

增广路径意味着有更大的值，$\min_{e \in E(P)} \epsilon(e)$

Definition(割)

在网络中，割 $[S,T]$ 包含了从 $S$ 到 $T$ 的边，且

$(T = V - S) \land(s \in S) \land (t \in T)$


Definition(割的容量)

$cap(S,T) = \sum_{u \in S, v \in T, uv \in E}c(u, v)$

即算 $S$ 与 $T$ 相连接的边的正向的容量之和

Definition(最小割)

最小割是拥有最小值的割

Theorem(弱对偶定理)

$val(f) \le cap(S, T)$

Lemma: 什么时候 $val(f) = cap(S,T)$?

1. 当流是最大流，即没有增广路径的时候。

2. 割是最小割，最小割的特点: $f^{-1}(S) = 0 \land f^+(S) = cap(S,T)$ (逆向为0，正向等于割的容量)

Theorem(强对偶定理)

$\max_{f}\ val(f) = \min_{[S,T]}\ cap(S,T)$

Theorem

一个可行流是最大流 $\iff$ 图中没有 $f$ - 增广路径

Method

重复寻找增广路径直到没有增广路径存在，就可以得到最大流

Algorithm

广度优先搜索(BFS)，寻找增广路径。直到没有增广路径的存在。

---

13 群论：群的基本概念

Definition(Group(群))

群 $(G, *)$ 是集合 $G$ 和一个抽象的操作 $*$ 满足下面的四个群的基本条件

1. 封闭：

   $$

   $$

   $$

   $$

   $$

   $$

   $$

   $$

Remark:

1. $a^0 = e$
2. $a^{-n} = (a^{-1})^n$

Definition(交换群、阿贝尔群)

$(G, *)$ 是一个群，如果 $*$ 满足交换律

$\forall a, b \in G.a*b = b*a$

那么 $(G, *)$ 是一个交换群。

Theorem

${\color{Red} G}$ 是一个群

1. 单位元是唯一的
2. 群中每个元素的逆元也是唯一的
3. $\forall a \in G.(a^{-1})^{-1} = a$
4. $\forall a, b \in G.(ab)^{-1} = b^{-1}a^{-1}$
5. $\forall a, b, c \in G.(ab = ac \Longrightarrow b = c) \land (ba = ca \Longrightarrow b = c)$ （消去律）
6. $\forall a, b \in G. \exists! x \in G. ax = b \land ya = b$

Definition(模 $m$ 剩余类乘法群)

$U(m) = \{a \in \mathbb{Z}_m |\ (a,m) = 1\}$

$a,m$ 的最大公约数为1。

Theorem

$(a,b) =d \Longrightarrow \exists u, v \in \mathbb{Z}.au + bv = d$

Theorem

当 $p$ 是一个素数：

$\mathbb{Z}^{*}_p = U(p) = \{1,2,\dots,p-1\}$

$\big\vert U(m)\big\vert = \varphi(m)$

表示小于 $m$ 的所有素数总共有多少

Definition

$\varphi = n \prod (1 - \frac{1}{p})$

$n$ 整除 $p$，且 $p$ 是素数，取所有 $p$ 相乘

Theorem

$G$ 是一个阿贝尔群且阶为 $n$（即群的大小）

$\forall a \in G. a^n = e$

Theorem(欧拉定理)

$m \in \mathbb{Z^+},a \in \mathbb{Z}$ 如果 $(a, m) = 1$，那么

$a^{\varphi(m)} = 1\ \ mod\ m$

Theorem(费马小定理)

如果 $p$ 是素数，那么对任意 $a \in \mathbb{Z}^+$

$a^{p-1} = 1\ mod\ p$

---

14 群论：子群

Definition(Subgroup(子群))

$(G, *)$ 是一个群且 $\emptyset \neq H \subseteq G$

如果 $(H, *)$ 是一个群，那么称 $H$ 是 $G$ 的子群，记作 $H \le G$

Theorem

如果有群 $H \le G$

1. $H$ 的单位元 $e$ 跟 $G$ 的单位元 $e'$ 相同

   $$

   $$

   $$

   $$

$G$ 是群且 $\empty \ne H \subseteq G$，那么 $H \le G \iff$

$\forall a, b \in H.ab^{-1} \in H$

如何证明一个群是子群

Theorem

$H_1 \le G$，$H_2 \le G$ $\Longrightarrow$

$H_1 \cap H_2 \le G$

Definition(对称群)

$M \ne \empty$ 是一个集合，$M$ 中所有的双射函数构成的集合，操作为复合，组成一个群，叫做 $M$ 的对称群。

$M = \{1,2,\dots,n\} \\ S_n = Sym(M)$

Remark：$\varphi \phi \neq \phi \varphi \qquad$两个都是对称群

Definition(轮换表示法)

Definition(置换群)

对称群的子群叫做置换群

Definition(陪集)

$H \le G$，对于 $a \in G$

$aH = \{ah | h \in H\}, \quad Ha = \{ha | h\in H\}$

叫做 $H$ 在 $G$ 中的左陪集和右陪集。

Theorem

$H \le G, a, b \in G$

1. $|aH| = |H| = |bH|$
2. $a \in aH$
3. $aH = H \iff a \in H \iff aH \le G$
4. $aH = bH \iff a^{-1}b \in H$
5. $\forall a, b \in G.(aH = bH) \lor (aH \cap bH = \emptyset)$

Theorem(拉格朗日定理)

$H \le G$。那么

$\big\vert G \big\vert = [G:H]·[H]$

群 $G$ 的大小等于陪集 $H$ 的大小乘 $\times$ 陪集的个数

Definition(Index(指标))

$G / H = \{gH\ |\ g \in G\} \\ [G: H] = |G/H|$

Remark：

$H \le G \Longrightarrow |H|\ \big\vert\ |G|$

即群 $G$ 的大小整除子群 $H$ 的大小

Definition(正规子群(Normal Subgroup))

$H \le G$。如果

$\forall a \in G. aH = Ha,$

那么 $H$ 是 $G$ 的正规子群，记作 $H \lhd G$

$aH = Ha \Longrightarrow \forall h \in H. \exists h' \in H.ah = h'a$

不能推出 $ah = ha$

Theorem

$H \lhd G \iff \forall a \in G. h \in H.aha^{-1} \in H$

证明正规子群：

1. 先证明群 $H$ 是子群
2. 然后用这个定理证明群 $H$ 是正规子群

Theorem(正规子群的陪集)

$H \lhd G$

$G / H = \{aH\ |\ a \in G\}$

叫做 $H$ 在 $G$ 的陪集

Definition(商群)

$H \lhd G$。定义

$aH \cdot bH = (ab) H$

那么 $(G/H, \cdot)$ 是一个群，叫做 $G$ 通过 $H$ 的商集，记作 $G / H$

Definition(同态)

$(G, \cdot),(G',*)$ 是两个群。$\phi$ 是一个函数且：

$\forall a, b \in G.\phi(ab) = \phi(a)\phi(b)$

那么 $\phi$ 是从 $G$ 到 $G'$ 的同态映射(homomorphism)

如果 $\phi$ 是双射函数，那么称为同构 $\phi:G \cong G'$

$\phi(ab)$ 中 $ab$ 的运算是 $G$ 中的运算， $\phi(a)\phi(b)$ 中的运算是 $G'$ 的运算

即 $\phi(a \cdot b) = \phi(a) * \phi(b)$

Theorem

$\phi$ 是 $G$ 到 $G'$ 的同态映射，$e$ 和 $e'$ 是 $G$ 和 $G'$ 的单位元，那么

1. $\phi(e) = e'$
2. $\phi(a^{-1}) = (\phi(a))^{-1}$

Theorem

1. $$

   $$

   H \lhd G \Longrightarrow \phi(H) \lhd G’

   $$

   K \le G’ \Longrightarrow \phi^{-1}(K) \le G

   $$

   K \lhd G’ \Longrightarrow \phi^{-1}(K) \lhd G

   $$

$\phi$ 是 $G$ 到 $G'$ 的同态映射， $e'$ 是 $G'$ 的单位元

$\phi^{-1}(\{e'\}) = \{a \in G\ |\ \phi(a) = e'\}$

叫做 $\phi$ 的核(kernel)，记作 $\ker \phi$

$\ker \phi \lhd G$

Theorem(群同态基本定理)

$\phi$ 是从 $G$ 到 $G'$ 的同态映射，那么

$G / \ker \phi \cong \phi(G)$

同态核可以看作群 $G$ 与其同态像 $\phi(G)$ 之间相似程度的一种度量

---

15 复习和补充

1. $\leftrightarrow,\rightarrow$ 用于单个公式之中(即公式内部)

2. $\Longleftrightarrow, \Longrightarrow$ 用于连接两个公式(推导公式的过程中使用)

3. 异或 $p \oplus q = (p \lor q) \land \lnot(p \land q) = (p \land \lnot q) \lor (\lnot p \land q)$

   满足交换律和结合律

4. $\sqrt{2}$ 是无理数(反证法)

   假设 $\sqrt{2} = \frac{p}{q}$ 且 $p, q$ 没有公因子

   $\Longleftrightarrow$ $2 = \frac{p^2}{q^2}$

   $\Longleftrightarrow$ $2q^2 = p^2$

   $\Longleftrightarrow$ $p$ 是偶数

   $\Longleftrightarrow$ $p$ 可以写成 $p = 2k$

   $\Longleftrightarrow$ $q = \sqrt{2}k$

   所以 $p, q$ 有公因子，这与假设矛盾，可以得证 $\sqrt{2}$ 为无理数

5. 鸽笼原理

   $n$ 个东西放进 $r$ 个盒子中，且 $r < n$，那么至少有一个盒子要放 $\ge 2(\ge \left\lceil\frac{n}{r} \right\rceil)$

6. 运用前序和来解决鸽笼问题的相关问题

7. 容斥原理

   1. $$

      $$

      |A \cup B \cup C| = |A| + |B| + |C| \
      • |A\cap B| - |A \cap C|-|B \cap C| \
      • |A\cap B\cap C|

      $$

Definition(自反闭包、对称必包、传递闭包)

1. 自反闭包：$R \subseteq X \times X$ 的自反闭包 $\text{cl}_{\text{ref}}(R)$ 满足下列条件：

   1. $R \subseteq Y$
   2. $Y$ 是自反的
   3. $Y$ 是满足前面两个条件的最小关系

   $\text{cl}_{\text{ref}}(R) = R \cup I_X$

2. 对称闭包：$R \subseteq X \times X$ 的对称闭包 $\text{cl}_{\text{sym}}(R)$ 满足下列条件：

   1. $R \subseteq Y$
   2. $Y$ 是对称的
   3. $Y$ 是满足前面两个条件的最小关系

   $\text{cl}_{\text{ref}}(R) = R \cup R^{-1}$

3. 传递闭包：$R \subseteq X \times X$ 的对称闭包 $\text{cl}_{\text{trn}}(R)$ 满足下列条件：

   1. $R \subseteq Y$
   2. $Y$ 是传递的
   3. $Y$ 是满足前面两个条件的最小关系

   $\text{cl}_{\text{trn}}(R) = R^+$

   $R^+ = \bigcup_{i = 1}^{\infin}R$ 即 $R^+ = R \cup R^2 \cup R^3 \cup \dots \cup R^{\infin}$

Definition(特征函数、自然函数)

1. 子集的特征函数

   已知 $A \subseteq X$，则：

   $$

   \chi_A(x) = 1 \iff x \in A

   $$

给两个偏序集 $(S, \le_S),(T, \le_T)$，从前者到后者的序上的同构是一个从 $S$ 到 $T$ 的双射函数，且满足：

$\forall x, y \in S.x \le_S y \leftrightarrow f(x) \le_T f(y)$

Definition(有根树、有向有根树)

Definition($k$ - 叉树、完全 $k$ - 叉树)

Algorithm(深度优先算法(DFS)遍历二叉树)

1. 前序：红色遍历: FBADCEGIH
2. 中序：绿色遍历: ABCDEFGHI
3. 后序：蓝色遍历: ACEDBHIGF

Algorithm(编码问题)

$F$ 为概率，$C$ 为对应要编码的对象

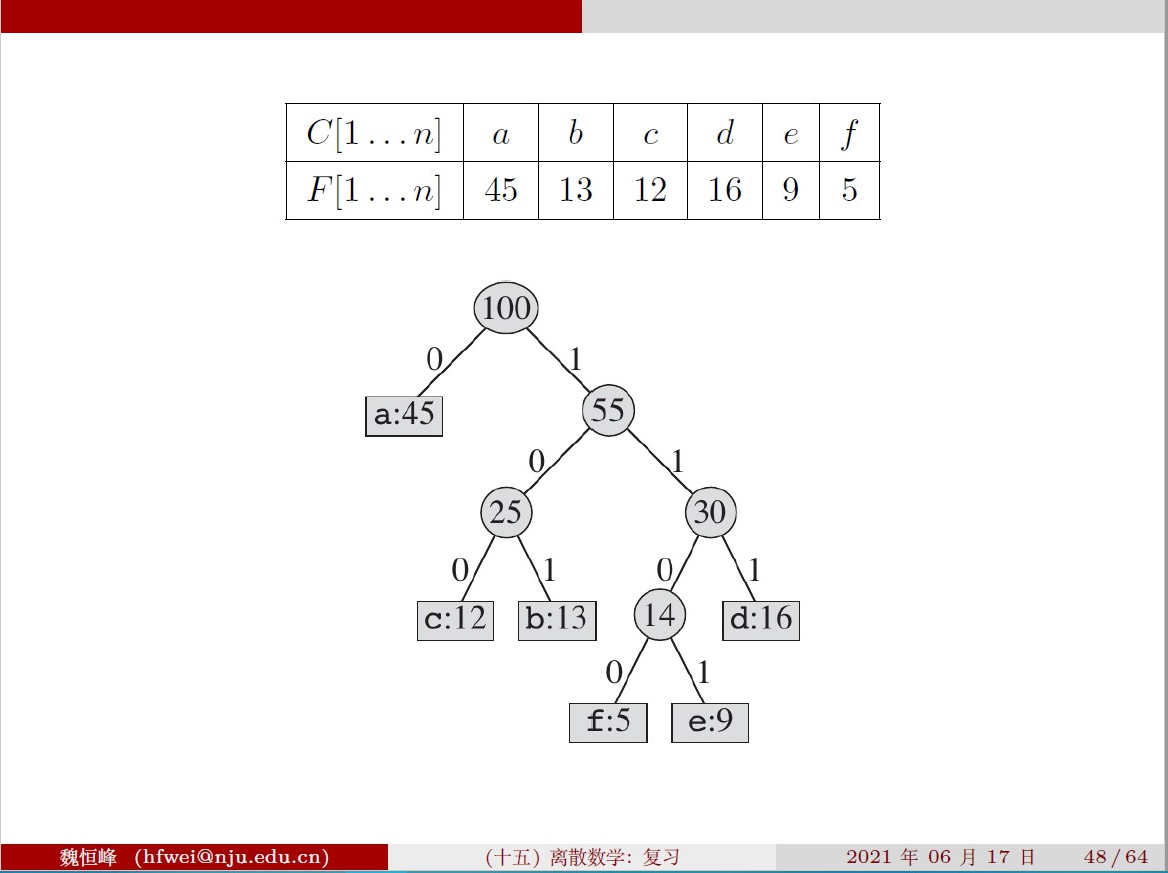
按递增顺序将出现的概率对应的字母排序，贪心选择出现次数最少的两个来组成二叉树的左孩子和右孩子(小的在左边)，这样重复之后将得到的树的左边标0，右边标1

Definition(对偶图)

平面图 $G$ 的对偶图 $G'$ 满足：

1. $G'$ 的每个顶点都在 $G$ 的一个面上
2. $G'$ 的每条边都跨越了两个不同的面(穿过 $G$ 的边)

Theorem

$G$ 是二部图 $\iff$ $\chi(G) = 2$ ($G$ 是 2-可着色的) $\iff$ $G$ 没有长度奇数的圈

Definition(色多项式)

Theorem

给定一个图 $G$ 和一条边 $e \in E(G)$，那么

$P(G, k) = P(G - e, k) - P(G/e, k)$

$G/e$ ：边的收缩，即将两个顶点收缩成一个顶点