1 计算机系统概述
What is computer
计算机是指通用电子数字计算机(general-purpose electronic digital computer)
- 通用:不是一种专用设备
- 所有计算机在给予足够时间和容量存储器的条件下,都可以完成同样的计算
- 当希望完成新的计算时,不需要对计算机重新设计
- 电子(非机械):采用电子元器件
- 数字(非模拟):信息采用数字化的形式表示
Organization and Architecture
- 组织(Organization):对编程人员不可以见
- 操作单元及其相互连接
- 包括:控制信号,存储技术,
- 例如:实现乘法是通过硬件单元还是重复加法(how to implement multiplication,编程人员不需要知道如何实现,只需要知道有加法这个东西,封装的实现就是组织)
- 结构(Architecture):对编程人员可见
- 直接影响程序逻辑执行的属性
- 包括:指令集,表示数据类型的位数,
- 例如:是否有乘法指令(是否有某种功能的接口,编程人员需要知道有这种接口才可以调用这种功能,这种就是结构)
History of computer
第一代 真空管(1946-1957)
-
ENIAC(1946-1955):第一台通用计算机,十进制,手动编程
-
ABC(1937):世界上第一台计算机,不可编程
-
EDVAC:冯·诺依曼结构
冯诺依曼结构
又称为“普林斯顿结构"
三个基本原则:
- 二进制
- 存储程序
- 5个组成部分
- 主存储器(存储单元):地址和存储的内容
- 算术逻辑单元(处理单元):执行信息的实际处理
- 程序控制单元(控制单元):指挥信息的处理
- 输入设备:将信息送入计算机中
- 输出设备:将处理结果以某种形式显示在计算机外
第二代 晶体管(1958-1964)
第三代及后续几代:集成电路(1965-现在)
思想:
-
将整个电路安装在很小的硅片上,而不是用分立元件搭成的等价电路
-
这些晶体管可以通过金属化过程相互连接,以形成电路
Moore‘s Law
摩尔定律:单芯片上所能包含的晶体管数量每年翻一番,1970年起减慢为每18个月翻一番
影响:
- 更小的尺寸带来更多灵活性和可能性
- 由于单个芯片的成本几乎不变,计算机逻辑电路和存储电路的成本显著下降
- 减小了对电能消耗和冷却的要求
- 集成电路上的内部连接比焊接更可靠,芯片间的连接更少
Computer Performance
计算机的关键参数之一:性能,成本,尺寸,安全性,可靠性,能耗
性能评价标准:
- CPU:速度
- 存储器:速度,容量
- I/O:速度,容量
计算机设计的主要目标是:提高CPU性能
CPU Performance
系统时钟
- 时钟频率 / 时钟速度(单位:Hz):计算机在单位时间内(例如1秒钟)执行的最基本操作的次数
- 时钟周期 / 周期时间(单位:s):执行每次最基本操作的时间
- 时钟滴答(有时也称为“时钟周期”):CPU中用于同步执行最基本操作的单个单子脉冲
- 因此,周期时间即为两个电子脉冲之间的时间
指令执行
-
处理器由时钟驱动,时钟具有固定的频率 ,或等价为固定的时钟周期
-
如果用 来表示执行指定类型 指令所需要的周期数,用 表示在某一给定程序中所执行的 类指令的条数,则可以计算整个的 如下:
-
执行一个给定程序的处理时间表示为:
T = I_c \times [p + (m \times k)] \times t
:存储器访问次数
:存储器周期时间和处理器周期时间之比
:在处理器和存储器之间传输数据
:时钟周期

- 每秒百万条指令(MIPS):
- 使用一系列基准程序来测量系统的性能
- 平均结果
- 算术平均值:
- 调和平均值:
2 计算机的顶层视图
冯诺依曼结构:存储单元,处理单元,控制单元,输入,输出
Computer Top-Level Structure
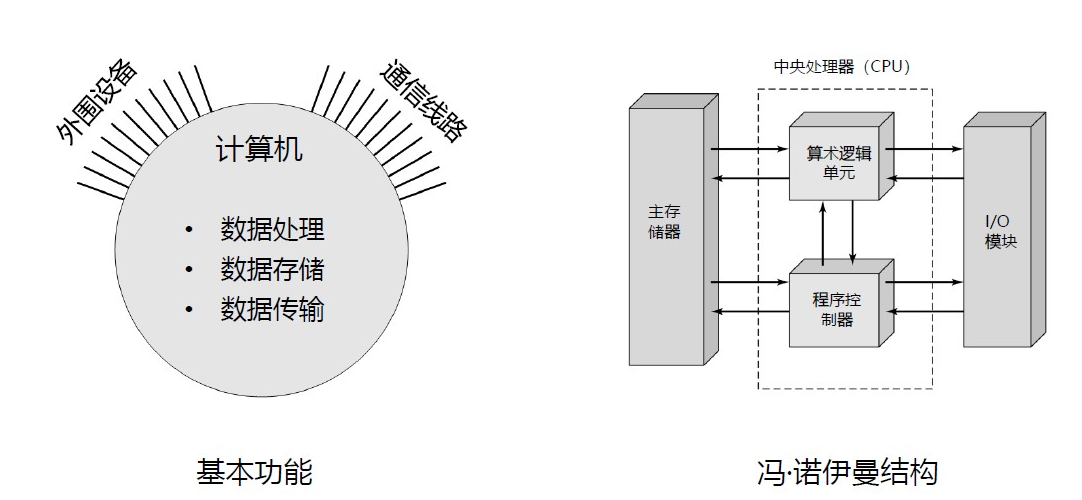
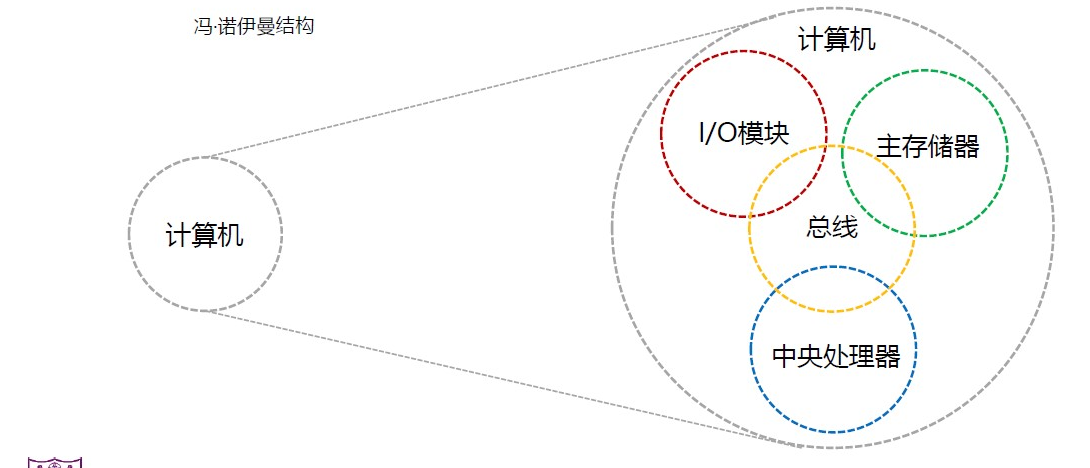
How Computer Works
-
指令和数据存储在单个读写存储器中
-
主存中的内容按位置访问,无需考虑其中包含的类型
位置:地址,存储的内容可以是数据也可以是指令也可以是地址
-
CPU从一条指令到下一条指令以顺序方式执行(除非明确修改)
-
I/O模块与CPU、主存交换计算机系统外部的数据
冯·诺依曼结构中的输入输出指的就是I/O模块,而不是外部设备
CPU
- CPU从一条指令到下一条指令以顺序方式执行(除非明确修改)
- 指令和数据存储在单个读写存储器中
- 主存中的内容按位置访问,无需考虑其中包含的类型
Q1:CPU的频率能不能无限提高
- 理论限制
- mos管开关、脉冲通过门电路需要时间
- 为了信号同步,每个脉冲信号需要持续一定的时间
- 制造限制
- 芯片面积越来越大,导致连线延迟越来越大,需要保证信号在设计指定时钟周期内从芯片的一角到达另一角
- 频率越高(即mos管的开关频率也越高)会导致开关损耗也越高,cpu会费电和散热高
- 解决:指令流水线,控制器,多核等
Q2:内存墙的存在
主存和CPU之间传输数据的速度跟不上CPU处理数据的速度(CPU发展速度远远快与主存发展的速度)
解决方法:采用高速缓存(Cache)
- 添加一级或多级缓存以减少存储器访问频率并提高数据传输速率
- 增大总线的数据宽度,来增加每次所能取出的位数
Q3:CPU等待I/O传输数据
CPU在等待I/O设备时保持空闲
解决方法:中断:其他模块(例如I/O)可以中断正常处理顺序的机制。将中断周期加入指令周期
Memory
- 指令和数据存储在单个读写存储器中
- 主存中的内容按位置访问,无需考虑其中包含的类型
Q4:兼顾存储容量、速度和陈本
-
约束
- 容量:越大越好
- 速度:跟上存储器处理数据的速度
- 成本:相对于其他组件合理
-
约束之间的关系
- 更短的访问时间,更高的每bit成本
-
解决方法:层次式存储结构(存储金字塔)
- 需求:
- 大容量数据存储
- 高速性能
- 解决方案:使用存储器层次结构而不是依赖单个存储器组件
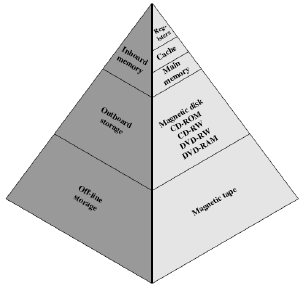
- 需求:
I/O
与CPU和内存交换从外部来源收集的数据(注意外部设备不能算是I/O中的东西,I/O指的是I/O模块,负责控制和传输)
Q5:I/O设备传输速率差异大
I/O性能跟不上CPU速度的提升
解决方法:采用缓冲区和改进I/O操作技术
Bus(总线)
总线时连接两个或多个设备的通信道路
Q6:计算机部件互联复杂
解决方案:采用总线
数据传输类型
- 控制线:控制数据线和地址线的访问和实用
- 地址线:指定数据总线和地址I/O端口上数据的来源或去向
- 数据线:在系统模块之间传送数据
3 数据的机器级表示
信息的二进制编码
在冯·诺依曼结构中,所有信息(指令和数据)都采用二进制编码
- 编码:用少量简单的基本符号对复杂多样的信息进行一定规律的组合
- 采用二进制的原因
- 多种物理器件可以表示两种稳定的状态,用于表示二进制中的 和
- 二进制的编码和运算规则简单
- 和 可以对应逻辑命题中的 “真” 和 “假”
- 位的二进制编码至多表示 个不同的值(无论是什么类型的数据都遵循这个规则)
整数的二进制表示
- 无符号整数
- 有符号整数:原码,反码,移码,补码
- 原码、反码、移码在进行加法运算时都会造成不必要的硬件需求,因此目前计算机中普遍使用补码
- 二进制补码的运算
- 二进制 - 十进制的转换
补码表示法
相比原码表示法的优势:无论同号还是异号都可以直接相加
表示:正数与原码相同,负数在对应原码的基础上**“取反加一”**
-
000…000 ~ 011…111:表示的值不变,与原码相同
-
100…000 ~ 111…111:表示的值由原来的 变为 (平移)
真值由原来的无符号数对应的真挚减去 ,取反加一的由来
补码的真值
值的范围:
浮点数的二进制数表示
-
实数表示
-
定点表示法表示值的范围是有限制的
-
科学计数法:
:尾数/有效值
:基/底,对所有数都是相同的,不需要存储的(隐含的)
:阶码/指数
规格化数
规格化表示:
-
符号总是位于字的第一位
-
尾数()的第 位总是 ,不需要存入尾数字段中(默认省略)
-
阶码()的真实值加上 后,再存入阶码字段中(移码)
假设阶码位数为,则偏移量计算如下:
-
底()默认为2
值的范围(未引入非规格化数的情况下)
- 介于 和 之间的负数
- 介于 和 之间的正数
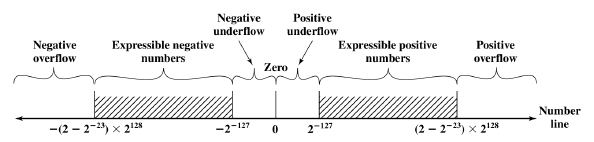
规格化数的变化
对于一定长度的规格化数,表示范围和精度之间存在权衡
- 增加阶码位数:扩大表示范围,降低表示精度
- 增加尾数尾数:提高表示精度,减少表示范围
- 采用更大的底:实现更大的范围,降低表示的精度
非规格化数
- 处理规格化数中的下溢情况
- 当结果的阶值太小时,通过右移进行非规格化;每次右移阶值增,直到阶值落在可表示范围内

IEEE754标准
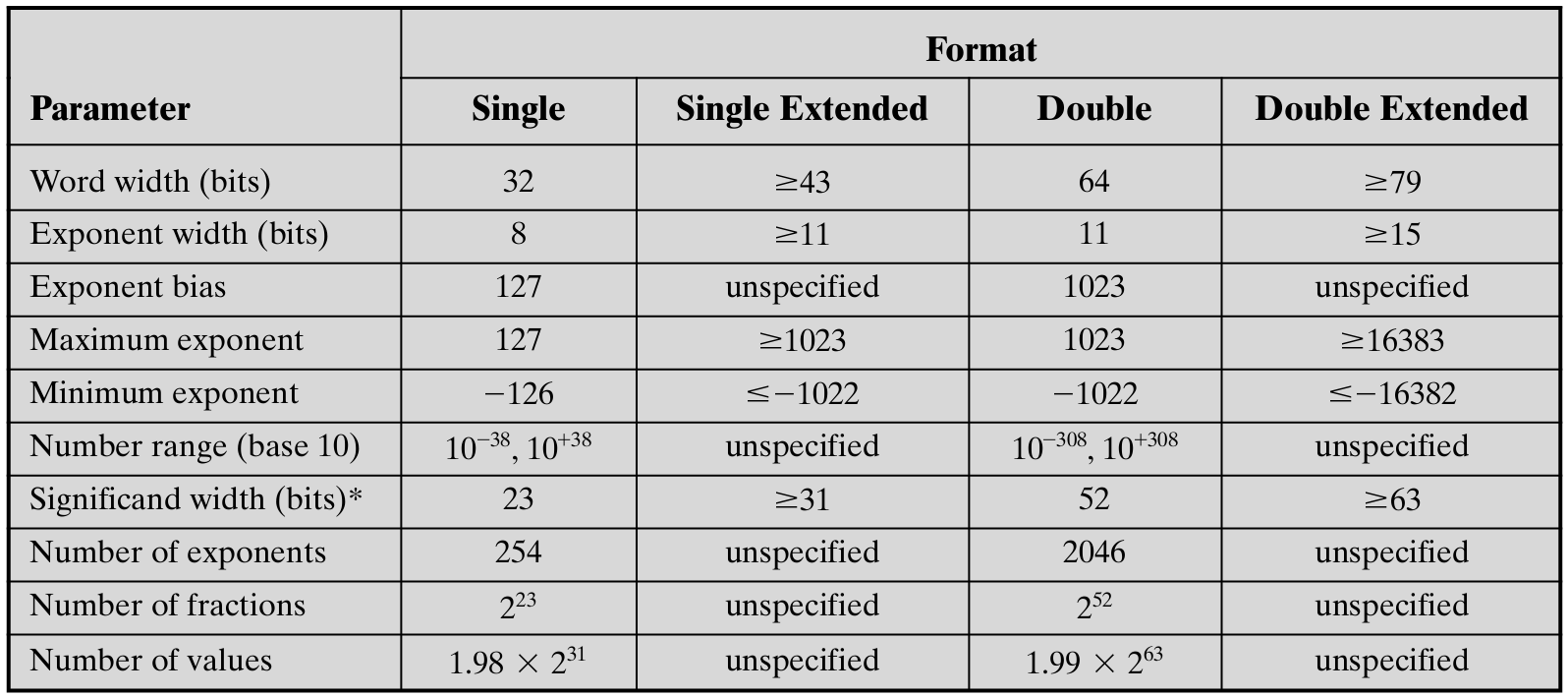
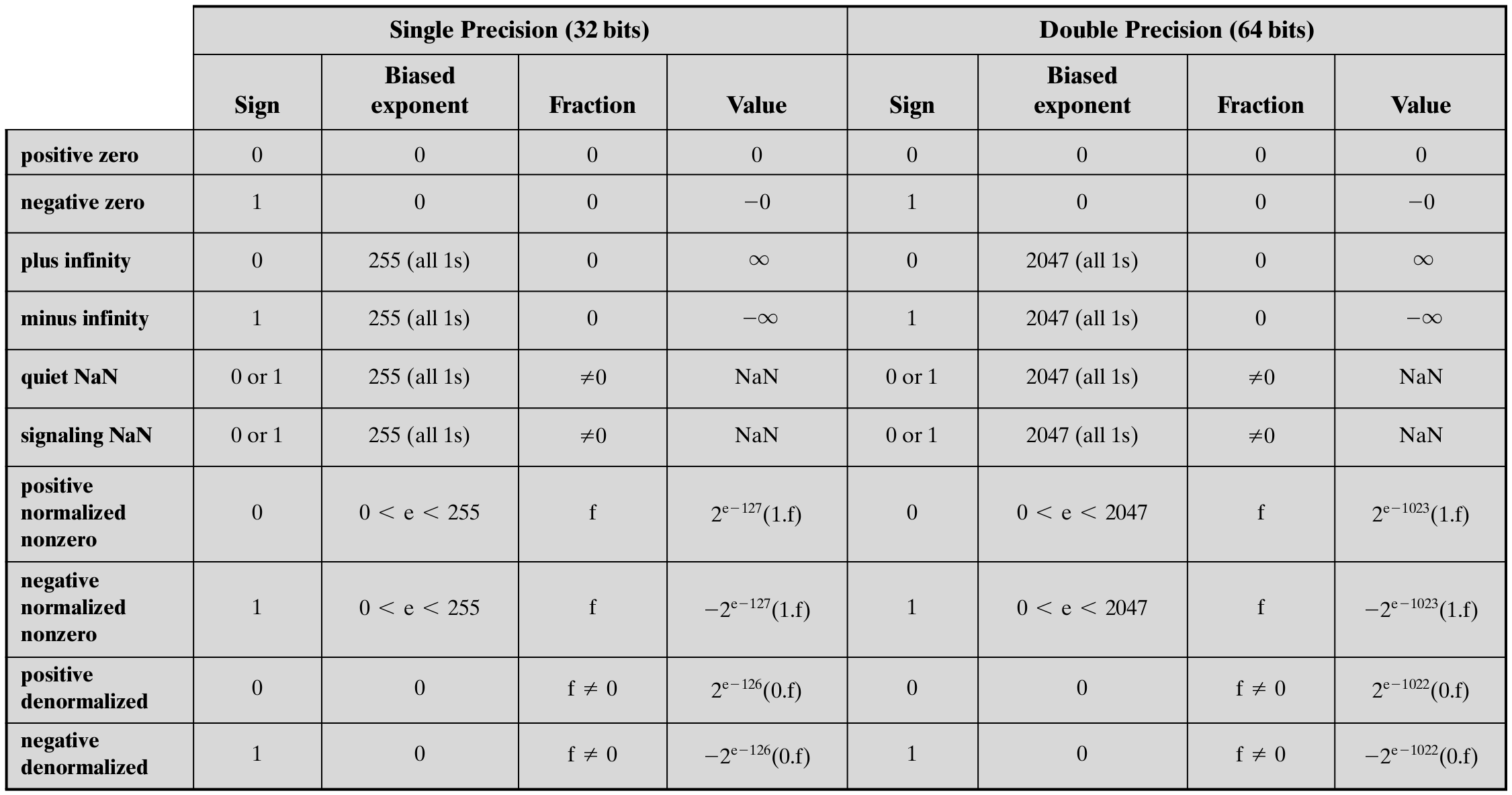
二进制编码表示的十进制数表示
- 浮点运算的问题:精度限制、转换成本高
- 应用需要:长数字串的计算
- 解决方法:用 位二进制编码十进制(BCD)表示 直接计算
NBCD码
- :
- 符号:使用四个最高有效位
- 正:
- 负:
4 数据校验码
差错(Error)
- 数据在计算机内部进行计算 、 存取和传送过程中 由于元器件故障
或噪音干扰等原因 会出现差错 - 以存储为例
- 硬故障(hard failure): 永久性的物理故障,以至于受影响的存储单元不能可靠地存储数据,成为固定的 或 故障或者在 和 之间不稳定地跳变
- 由恶劣的环境 、制造缺陷和旧损引起
- 软故障 (soft error):随机非破坏性事件,它改变了某个或某些存储单元的内容 但没有损坏机器
- 由电源问题或 α 粒子引起
- 硬故障(hard failure): 永久性的物理故障,以至于受影响的存储单元不能可靠地存储数据,成为固定的 或 故障或者在 和 之间不稳定地跳变
- 解决方案
- 从计算机硬件可靠性入手,在电路 、电源 、布线等方面采取必要的措施,提高计算机的抗干扰能力
- 采取数据检错和校正措施,自动发现并纠正错误
纠错(Error Correction)
-
基本思想:存储额外的信息以进行检错和校正
-
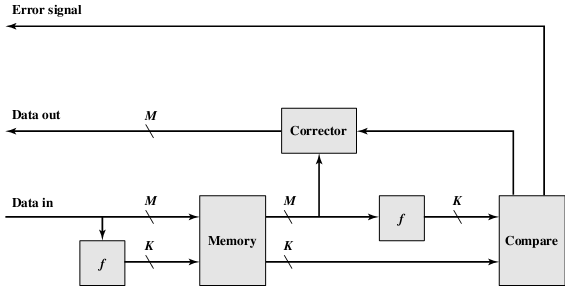
处理过程
-
数据输入:使用函数 在 位数据 上生成 位的校验码
-
数据输出:使用函数 在 位数据 上生成新的 位校验码 ,并与取出的 位校验码 进行比较
注意这里的 不一定等于 ,因为在数据存储的过程中校验码也有可能变化,所以我们进行比较的其实是取出后的校验码和将取出后的数据经过计算得到的校验码来判断是否有出错。
我们可以考虑一种特殊情况:如果在存储过程中数据和校验码同时出错,且数据出错后计算得到的校验码刚好是校验码出错后的结果,那么这种纠错就会失去作用。
不过幸运的是,在这里我们都假设只有一位会出错(无论数据还是校验码)。
- 没有检测到差错:使用数据 ( 可能不等于 )
- 检测到差错并且可以校正:校正数据 来生成数据 ,并用数据
- 检测到差错但无法纠正:报告
-
奇偶校验码
基本思想:增加一位校验码来表示数据中 的数量是奇数还是偶数
处理过程:
- 假设数据为
- 数据输入(奇校验的数据加入校验码后有奇数个 ,偶校验相反)
- 奇校验:
- 偶校验:
- 数据输出
- 奇校验:
- 偶校验:
- 检错:
- :正确 / 数据中出错的位数为偶数
- :数据中心出错的位数为奇数
优点:代价低,只需要1位额外数据,计算简单
缺点:
- 不能发现出错位数为偶数的情形
- 发现错误后不能校正
海明码
基本思想:将数据分成几组,对每一组都使用奇偶校验码进行检错
处理过程:
- 将 位数据分成 组
- 数据输入:为数据 中每组生成 位校验码,合并得到 位校验码
- 数据输出:为数据 中每组生成 位校验码,合并得到新的 位校验码
- 检错:将校验码 和取出的校验码 按位进行异或,生成 位故障字(syndrome word)
校验码长度
假设最多 位发生错误,数据的长度为 ,校验码长度为
可能的情况:
- 数据中有一位出现错误:
- 校验码中有一位出现错误:
- 没有出现错误:
校验码长度:
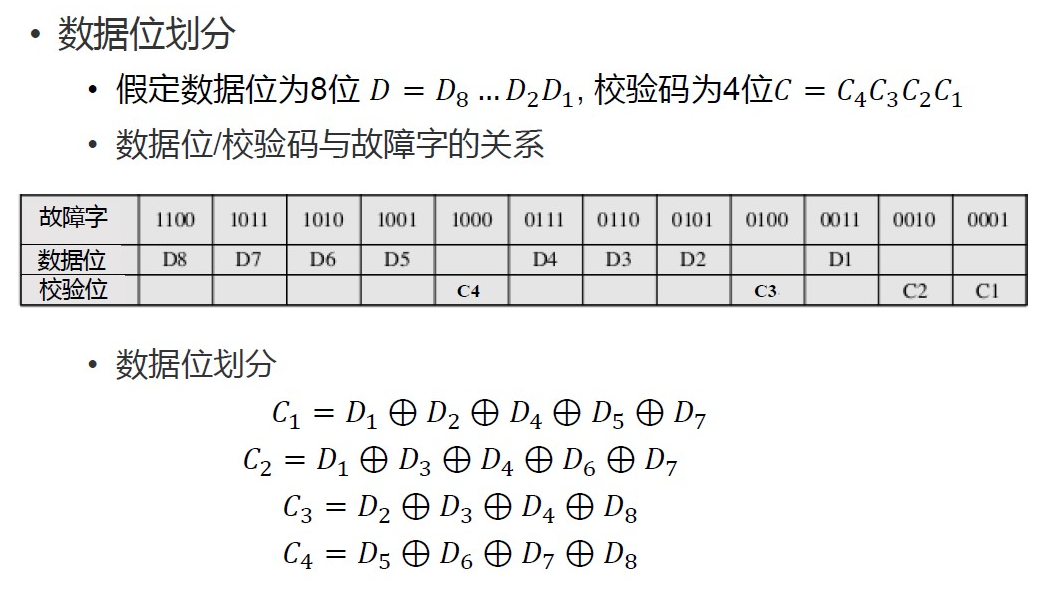
故障字
故障字的每种取值都反映一种情形(数据出错 / 校验码出错 / 未出错)
规则:
- 全都是0:没有检测到错误
- 有且仅有1位是1:错误发生在校验码中的某一位,不需要纠正
- 有多位为1:错误发生在数据中的某一位,将 中对应数据位取反即可纠正(得到)
将位设置在与其故障字值相同的位置
循环冗余校验(Cyclic Redundancy Check, CRC)
适用于以流格式存储和传输大量数据
用数学函数生成数据和校验码之间的关系
基本思想:
- 假设数据有 位,左移数据 位(右侧补 ),并用 位生成多项式除它(模 运算)
- 采用 位余数作为校验码
- 把校验码放在数据(不含补的0)后面,一同存储或传输
校错:
- 如果 位内容可以被生成多项式除尽,则没有检测到错误
- 否则,发生错误
模2运算
规则:有一落一,没一落零,做异或运算。
5 整数运算
算术逻辑单元(ALU)
算术逻辑单元是计算机实际完成数据算术逻辑运算的部件
- 数据由寄存器(registers)提交给ALU,运算结果也存于寄存器
- ALU可能根据运算结果设置一些标志(Flags),标志值也保存在处理器内的寄存器中
- 控制器(Control unit)提供控制ALU操作和数据传入送出ALU的信号
加法
全加器
- 与门延迟:1ty
- 或门延迟:1ty
- 异或门延迟:3ty
基本思想:第 位加法
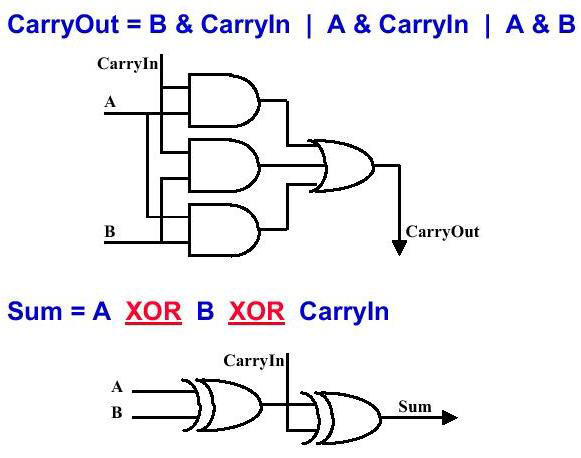
串行进位加法器
延迟:
计算 时,不需要等待 ,直接计算 ,需要6ty的延迟
计算 时, 的延迟是 2ty(按照公式),但此时 还没算完(需要3ty的延迟),所以仍然不需要等待 ,此时仍然只需要 6ty 的延迟
其余时刻,由于计算 的时候需要等待 ,在等待过程中可以先把 算好,因此只需要在 的基础上(计算 的延迟)再加上异或门的时间(3ty),因此
全先行进位加法器(CLA)
定义两个辅助函数:
延迟:6ty
- 先求所有的 和 ,需要 1ty(并行求)
- 再求所有的 ,需要2ty。
- 再与 的结果进行异或,因为前面两个的延迟和是3ty,所以 也同步完成,这里直接进行异或即可
部分先行加法器
思路:采用多个CLA并将其串联,取得计算时间和硬件复杂度之间的权衡。
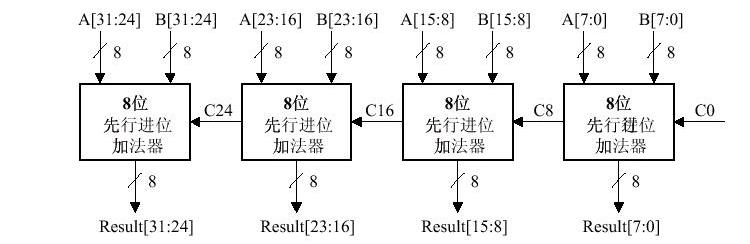
延迟:12ty
首先计算所有CLA中的 和 ,需要 1ty,然后计算第一个CLA中的 ,需要2ty,同时在这 3ty 中同步计算所有CLA中的 ,然后 传到第二个CLA中,第二个CLA计算 ,需要 2ty,第三个同理,同时在这4ty的延迟中,第一个CLA已经计算好了 。然后到最后一个CLA,同理计算 ,然后计算 ,同步进行的还有第二个和第三个CLA的计算 。(可以将四个CLA的计算 看成同步进行的)
overflow
减法
溢出与加法相同
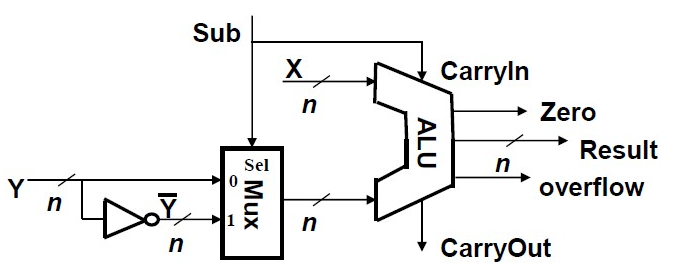
乘法
计算机乘法的改进
- 每一步都计算部分积求和结果
- 右移部分积代替左移部分积
- 若 ,只执行移位操作
问题:
布斯乘法
推导:

布斯乘法
- 增加
- 根据 ,决定是否增加
- 右移部分积(右移补充的是符号位)
- 重复步骤2和步骤3 次,得到最终结果
除法
不同情形的处理
- 若被除数为0,除数不为0:商为0
- 若被除数不为0,除数为0:发生“除数为0”异常
- 若被除数、除数均为0,发生“除法错”异常
- 其余情况进行进一步的除法运算
手工演算除法
- 在被除数的左侧补充符号位,将除数的最高位与被除数的次高位对齐
- 从被除数中减去除数,若够减,则上商为1;若不够减,则上商为0
- 右移除数,重复上述步骤
改进
- 右移除数编程左移余数/商
- 余数和商放在一个长度为 的寄存器中
如何判断够减:余数是否足够大
- 如果余数和除数的符号相同:减法
- 如果余数和除数的符号不同:加法
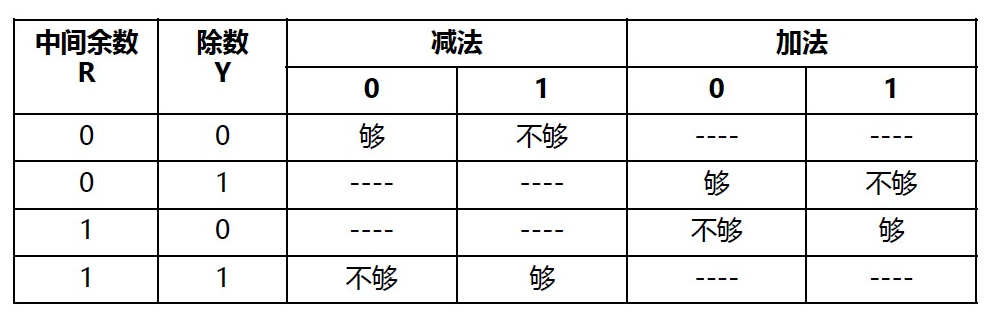
恢复余数除法
步骤过程
- 通过在被除数前面加 位符号扩展被除数,并存储在余数寄存器和商寄存器中
- 将余数和商左移,判断是否够减
- 如果“够”,则做减法(同号)或加法(异号),并上商为0
- 如果“不够”,则上商为0,并恢复余数
- 重复以上步骤
- 如果除数和被除数不同号,则将商替换为其相反数(商和被除数须同号)
- 余数存在余数寄存器中
不恢复余数除法
大致思路:不恢复余数,只考虑减法
- 如果余数 足够大:
- 如果余数 不够大:
步骤过程
- 通过在被除数前面加 位符号扩展被除数,并存储在余数寄存器和商寄存器中
- 如果除数和被除数符号相同,则做减法;否则,做加法
- 如果余数和除数符号相同,则商 ,否则
- 如果余数和除数符号相同,;否则,
- 如果新的余数和除数符号相同,使商为1,否则,使商为0
- 重复第三步
- 左移商
- 如果商是负的(被除数和除数的符号不同),商加1
- 余数和被除数符号不同,修正余数
- 若被除数和除数符号相同,最后余数加除数;否则,最后余数减除数
6 浮点数运算
加法和减法
步骤过程
- 检查0
- 对齐有效值(小阶对大阶)
- 加或减有效值
- 规格化结果
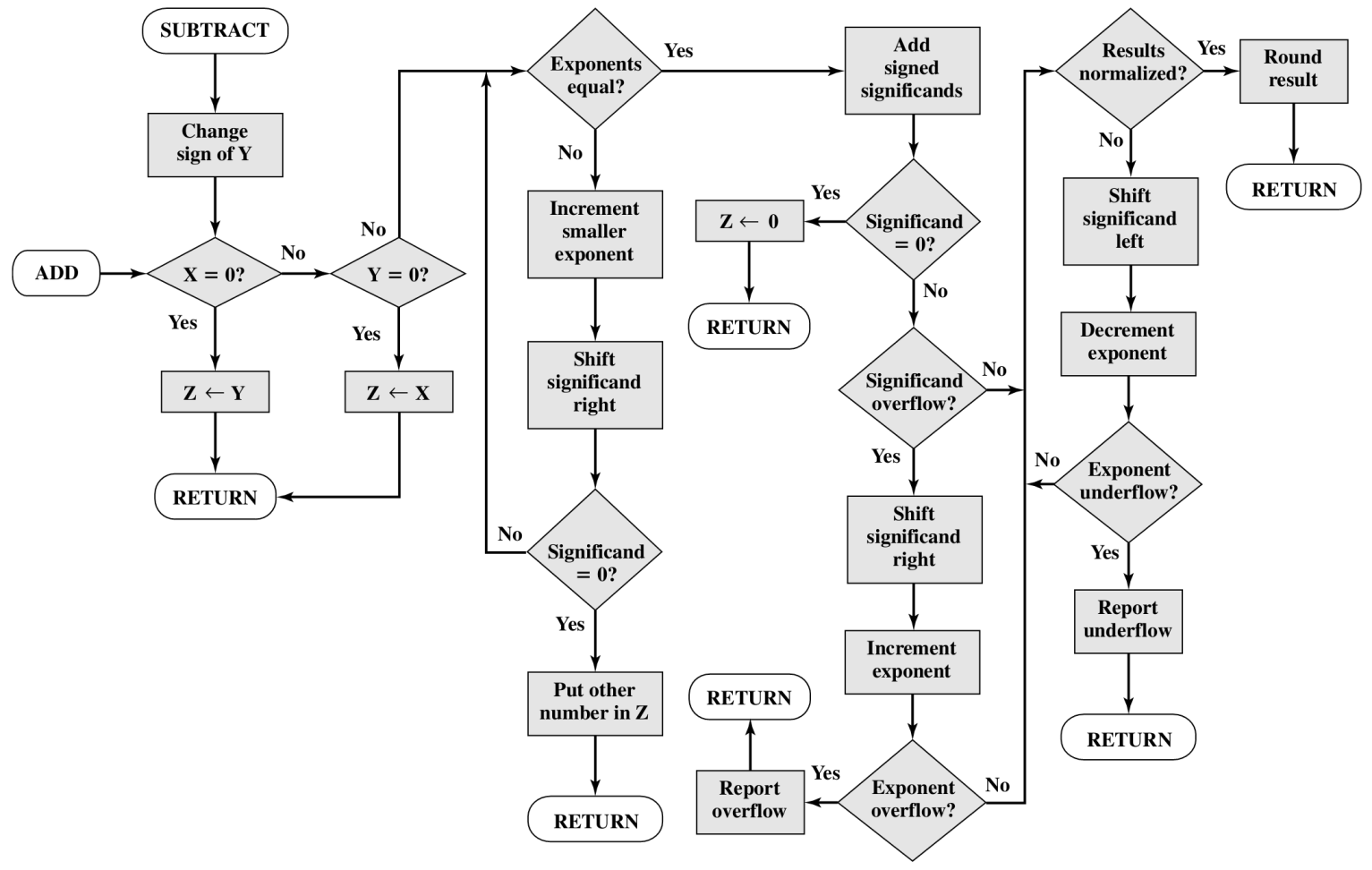
溢出
- 阶值上溢
- 正阶值超过可能的最大允许阶值
- 标记为 或者
- 阶值下溢
- 负阶值小于可能的最小允许阶值
- 报告为0
- 有效值上溢
- 同符号的两个有效值相加可能导致最高有效位的进位
- 通过重新对齐来修补
- 有效值下溢
- 在有效值对齐过程中,可能有数字被移出右端最低位而丢失
- 需要某种形式的四舍五入(保护位)
原码加法
如果两个操作数有相同的符号,做加法;否则,做减法
- 做加法:直接相加
- 如果最高位有进位,则溢出
- 符号和被加数(被减数)相同
- 做减法:加第二个操作数的补数
- 如果最高位有进位,正确(符号与被减数相同)
- 否则,计算它的补码(符号与被减数相反)
乘法
- 无论哪个操作数是0,乘积即为0
- 从阶值的和中减去一个偏移量()
- 有效值相乘
- 结果的规格化和舍入处理
- 规格化可能导致阶值下溢
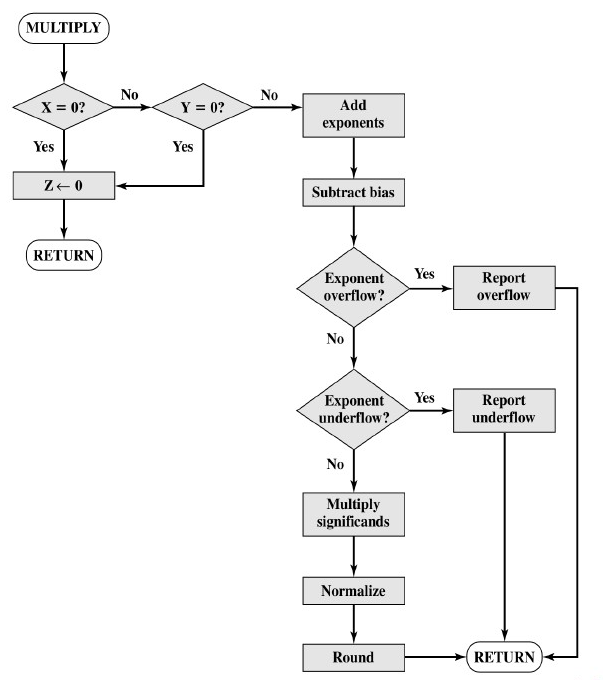
除法
- 如果除数为0,则报告出错,或将结果设置为无穷大
- 如果被除数是0,则结果是0
- 被除数的阶值减除数的阶值,加上偏移量()
- 有效值相除
- 结果规格化和舍入处理
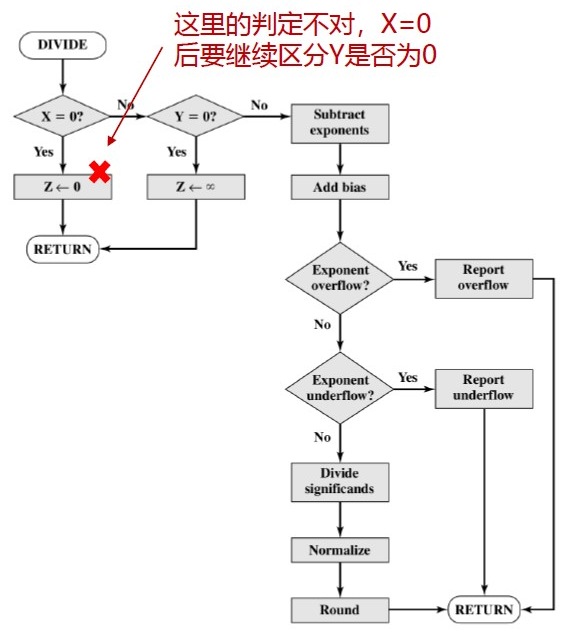
精度考虑
保护位:
- 寄存器的长度几乎总是大于有效值位长与一个隐含位之和
- 寄存器包含的这些附加位,称为保护位
- 保护位用0填充,用于扩充有效值的右端
舍入
- 对有效值操作的结果通常保存在更长的寄存器中
- 当结果转换回浮点格式时,必须要去掉多余的位
- 就近舍入:结果被舍入成最近的可表示的数
- 朝 舍入:结果朝正无穷大方向向上舍入
- 朝 舍入:结果朝负无穷大方向向下舍入
- 朝 舍入:结果朝 舍入
7 二进制编码的十进制数运算
加法
相加结果如果大于10,需要再加6来进位
- 10 ~ 15之间,不够进位,需要补6,
- 16 ~ 19 之间,已经进位,多减了6,需要补充一个6
减法
参照补码减法,避免借位
反转数字
参照补码的取反加一。有两种方法进行“取反”
- 按位反转,然后添加“1010”
- 添加“0110”,并按位反转
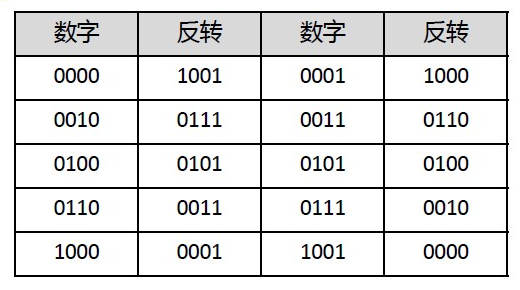
结果调整
- 如果有进位,舍弃进位,正确
- 如果没有进位,说明不够减,则对结果按位反转之后加一,并将结果符号取反