链接预测简介

链接预测主要用在图数据当中，无论是社交网络、媒体网络或者信息网络都可以看作图数据，链接预测的主要功能是基于已有的链接来预测未来在图数据网络中可能出现的链接以及链接跳转的可能性。比如网页间的跳转就可以将各个网页构成一个图，如何预测某个网页会被访问到的概率以及如何对这些网页做一个排序和推荐（以便搜索引擎进行推荐等功能），就是1链接预测的功能。

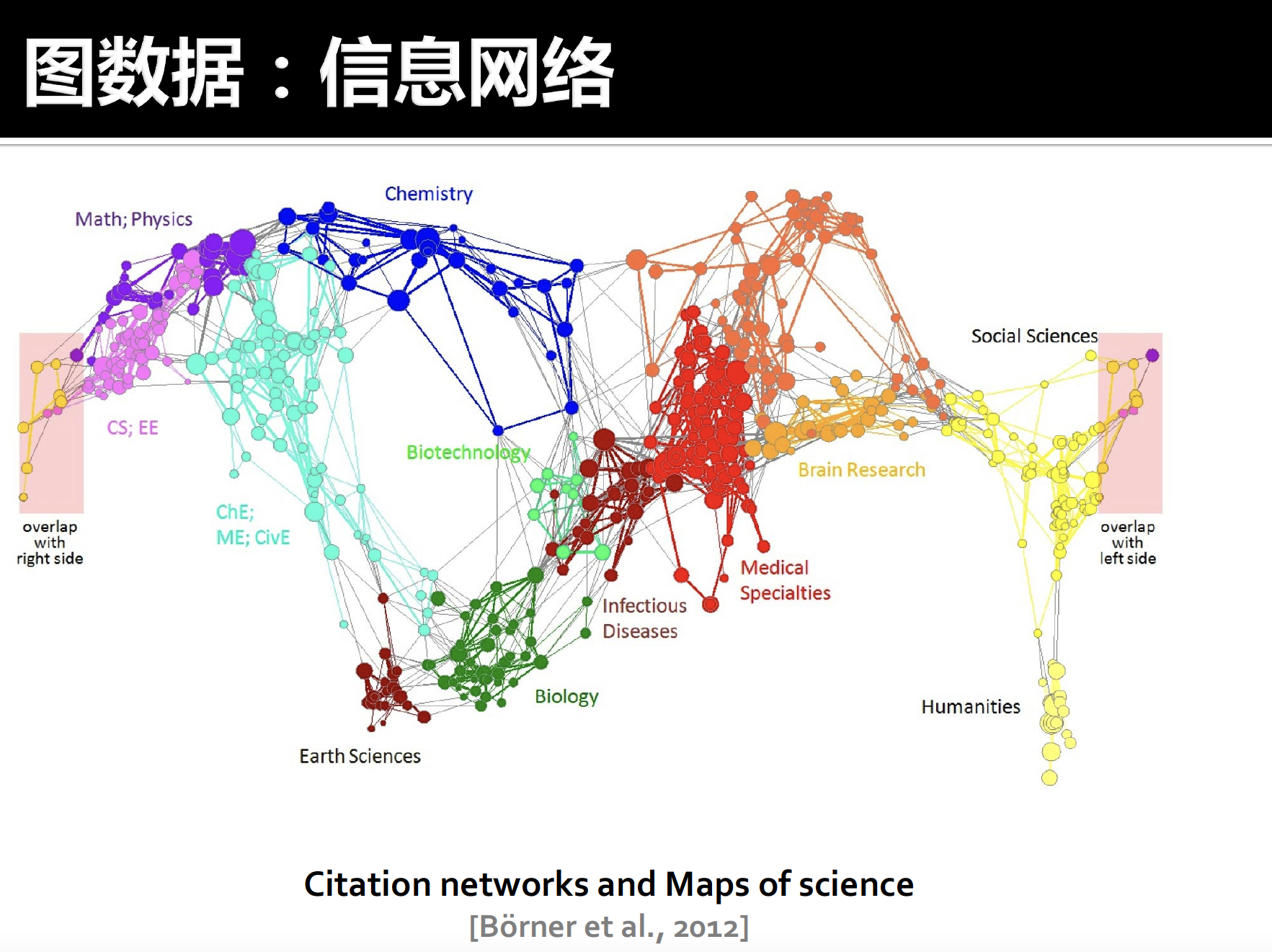
网页数据

如何将 Web 表示为有向图？

• 节点：网页
• 边：超链接

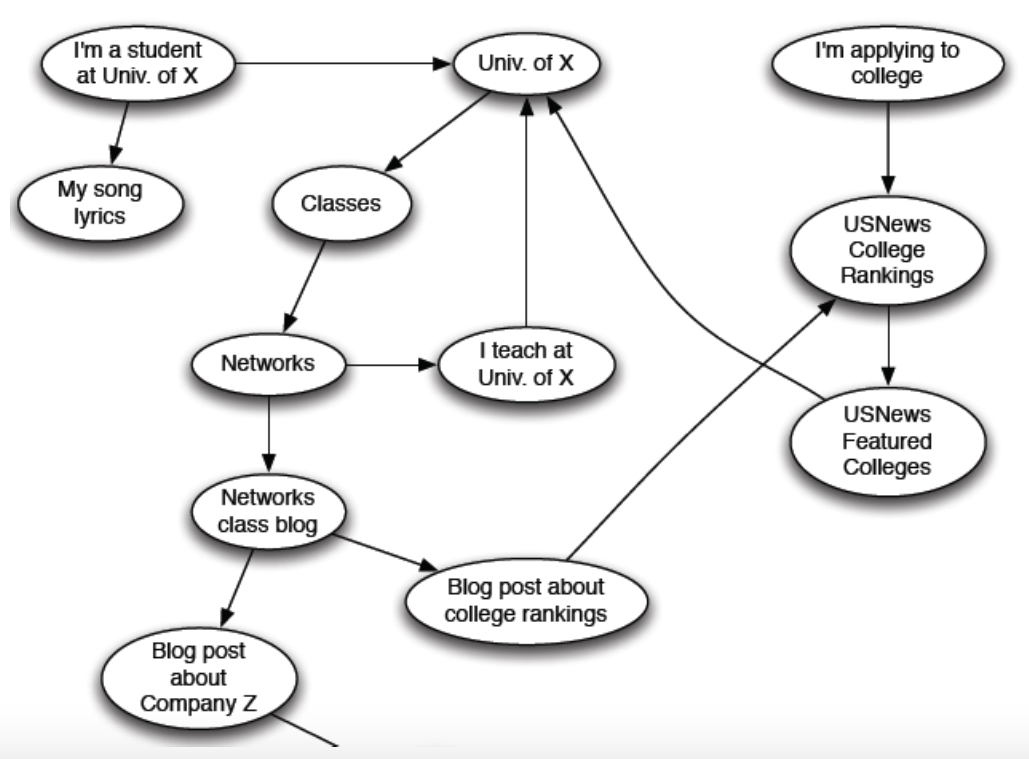
网页搜索存在的问题：

1. 网络中存在很多回答，到底应该相信哪个回答？
2. 查询“数据”的最佳的回答是什么

此时就需要链接预测算法来发挥作用，将网页看作是有权重的，权重越大的网页被认为越能够被信任。下面将介绍链接预测的一种算法：PageRank

PageRank 算法

算法思想：某个页面拥有的链接越多则越重要，需要注意的是并不是所有链接都是相同比重的，而是递推的。

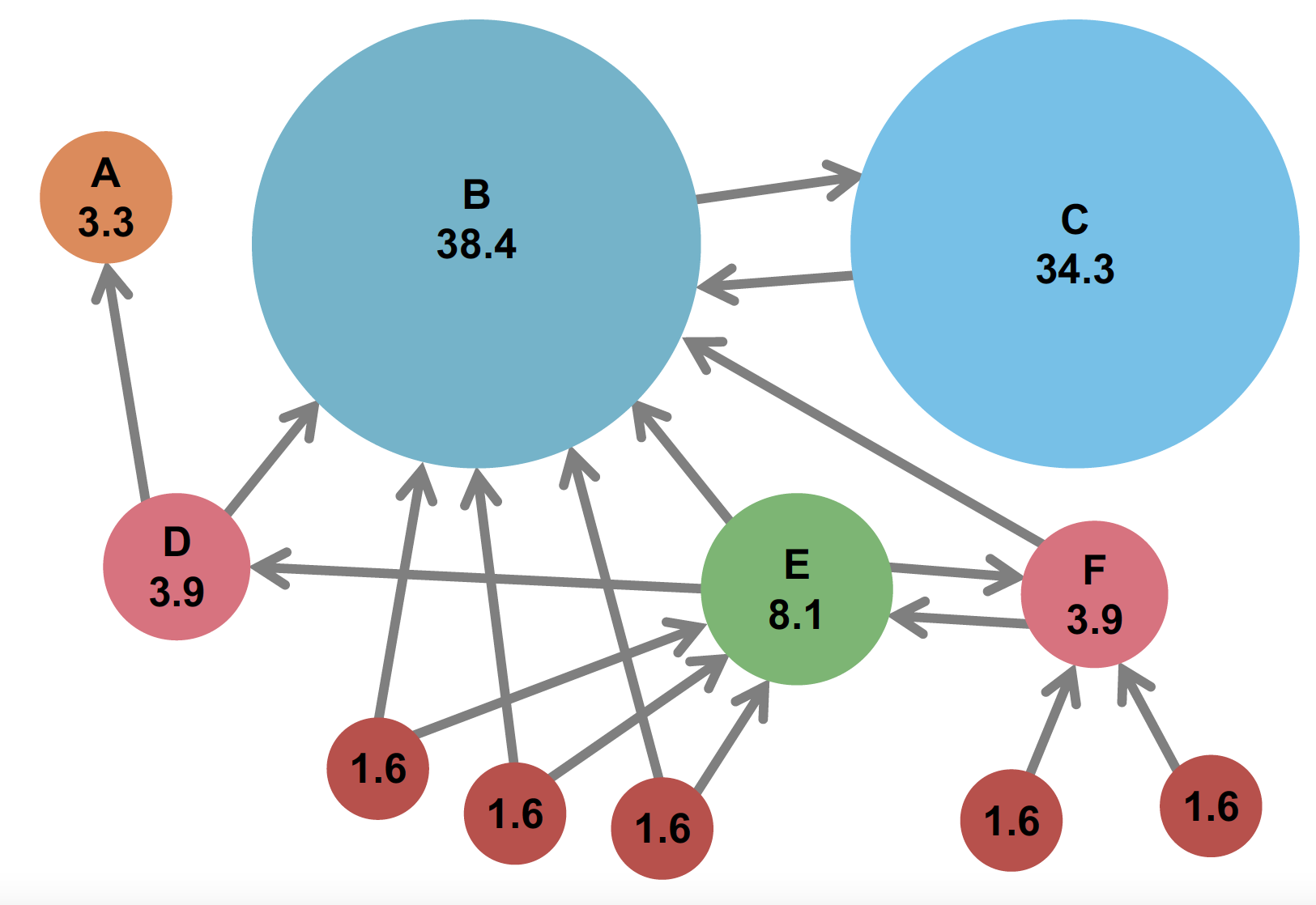
算法流程：

假设有 $n$ 个网页（即 $n$ 个节点）

1. 计算转移矩阵：转移矩阵 $M$ 是一个 $n \times n$ 的矩阵，$m_{ij}$ 定义为从 $j$ 网页流向 $i$ 网页占 $j$ 网页的所有出链的比例（即 $\frac{j \rightarrow i 的路径数量}{j 的所有出链数量}$）。
   1. 易知，转移矩阵 $M$ 的每一列的和为 1
   2. 转移矩阵 $M$ 的每一个元素的范围都在 $[0, 1]$ 之间
2. 迭代的计算链接评分，$PR(i+1) = M PR(i)$（其中 $PR(0) = \frac{ee^T}{n}$，$n$ 为节点数量）

下面通过一个例子来分析：

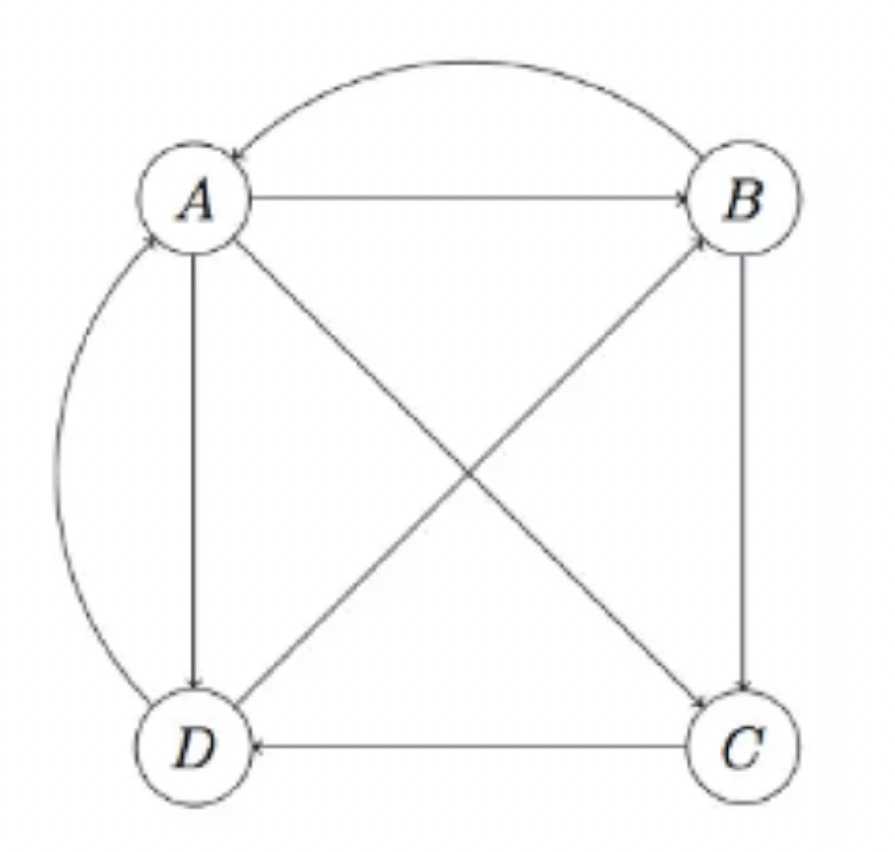
Dead Ends 问题

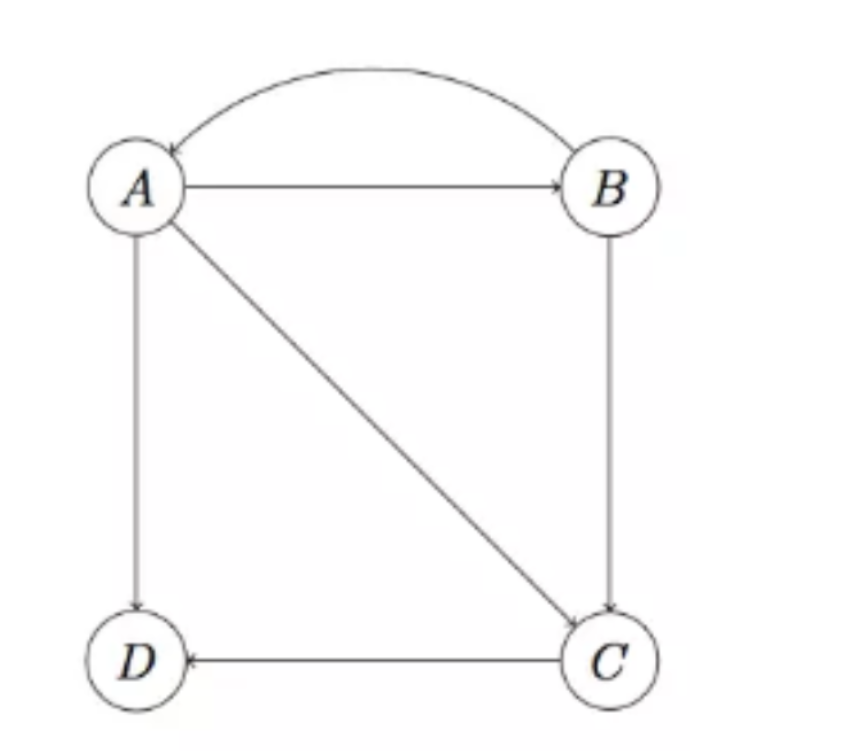
Dead Ends 是指某个节点没有任何的出链（out-links）在迭代过程中 PageRank 会逐渐变为0。

使用 teleport 解决 Dead Ends 问题，即对于转移矩阵中有一列全为0的情况，再加上一个 $a^T(\frac{e}{n})$（$e$ 是单位矩阵，$a$ 是只有 dead Ends 所对应的列为 1，其余全为 0 的矩阵，n 是个数）

Spider Trap 问题

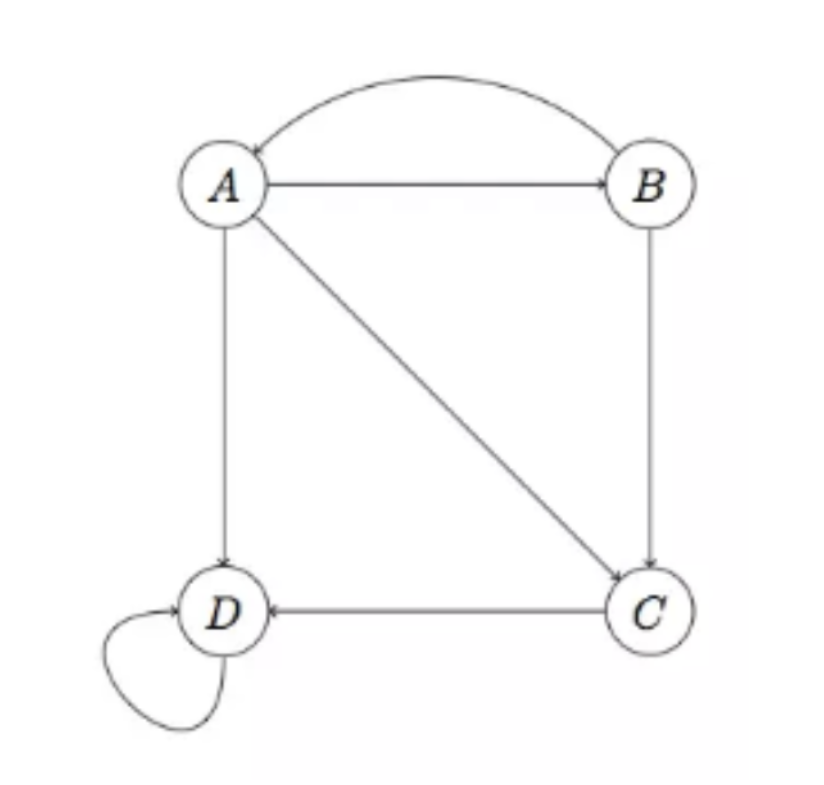
节点与其他节点之间没有 out-links，会导致网站的权重变为向一个节点偏移。

解决方法为使用 Random Teleport。一般 $\beta = 0.8$，$M = \beta M + (1 - \beta)\frac{ee^T}{n}$

Reference

1. link prediction predict edges in a network using networkx
2. PageRank 和 Dead Ends、Spider Trap 问题