Dynamic Programming

动态规划的概念

动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题

即，将问题拆分成子问题，直到子问题可以解决，然后将子问题的答案保存起来以达到减少重复计算的目的。再根据子问题答案反推，得出原问题答案

动态规划的核心思想

拆分子问题
记住过往
减少重复计算

动态规划的例子——青蛙跳台阶问题

该问题来自Leetcode 剑指Offer 10- II. 青蛙跳台阶问题

问题描述：一个青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 $n$ 级的台阶总共有多少种跳法

Method One: 暴力递归

思路

我们可以先举一个简单的例子。

要想跳上第十级台阶，有两种方法，一种是先跳到第九级台阶然后再跳一级台阶，另一种是跳到第八级台阶然后再跳两级台阶。我们设跳到第 $n$ 级台阶的跳法为 $f(n)$ ，那么我们可以得到 $f(10) = f(9) + f(8)$
要想跳上第九级台阶，也是要么从第八级台阶再跳一级，要么从第七级台阶再跳两级。即 $f(9) = f(8) + f(7)$
$\dots$

很明显我们可以的得到以下的公式，即 $f(n) = f(n - 1) + f(n - 2)$ 也就是斐波拉契数列的一个递推式。对于 $f(1)$ ，显然知道 $f(1) = 1$ ，对 $f(0)$ ，显然知道（或者我们定义）其值也为 $1$ 。

于是我们有了以下采用递归写出来的解法

class Solution {
    public int numWays(int n) {
        if (n == 1) {
            return 1;
        } else if (n == 0) {
            return 1;
        } else {
            return numWays(n - 1) + numWays(n - 2);
        }
    }
}

问题

如果我们在Leetcode上提交，会发现这个代码是AC不了的，会超过时间限制。这是为什么呢？让我们来看看该问题的递归树(图片来自知乎)

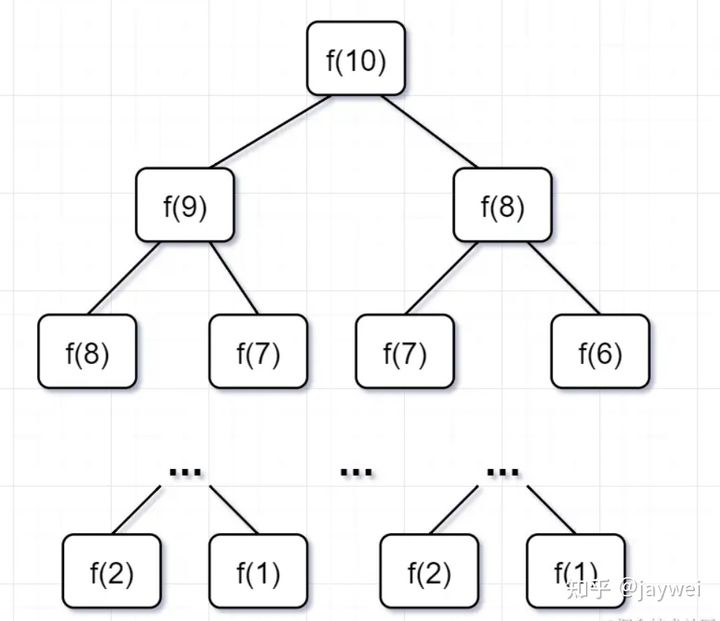
可以很明显看到，要解决 $f(10)$ ，就要计算出 $f(9)$ 和 $f(8)$
要计算出 $f(9)$ ，就要计算出 $f(8)$ 和 $f(7)$
一直计算到 $f(1)$ 和 $f(0)$ ，递归树才终止

可以计算出该递归的时间复杂度 = $O(2^n)$

递归时间复杂度 = 解决一个子问题的时间 * 子问题的个数

这里解决子问题的时间是加法操作，复杂度为 $O(1)$ 。

问题个数 = 递归树节点个数，总结点为 $2^n - 1$

指数级别的复杂度， $n$ 较大的时候超时就算是比较正常的了。回过头来看，会发现其中存在着大量的重复计算。既然有大量重复计算，我们就可以先存储第一次计算时得到的值，如果后面有用到的话直接取就可以啦。这也是我们的第二种解法。

Method Two：带备忘录的递归解法(自顶向下)

我们一般使用一个数组或者一个哈希Map来充当这个备忘录

思路

即在第一次计算的时候将计算所得的值添加到哈希表当中
后续的计算中如果该值已经在哈希表中，我们就可以直接取该值，而不用再去重复计算。
实际上还是递归的思想，只是我们新加了将已经计算过的值存储起来。

因此我们可以得到如下代码：

class Solution {
	// 使用哈希map来充当备忘录的作用
    Map<Integer, Integer> recording = new HashMap<>();
    
    public int numWays(int n) {
        if (n == 0) {
            return 1;
        } else if (n <= 2) {
            return n;
        } else if (recording.containKey(n)) {
            return recording.get(n);
        } else {
            // 取模是题目的要求
            recording.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);
            return recording.get(n);
        }
    }
}

Method Three: 动态规划(自底向上)

思路

动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也是差不多呢。两者的差别在于：

带备忘录的递归，是从 $f(10)$ 往 $f(1)$ 方向延伸求解的，所以也称为自顶向下的解法。
动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从 $f(1)$ 往 $f(10)$ 方向，往上推求解，所以称为自底向上的解法

动态规划的典型特征

最优子结构
状态转移方程
边界
重叠子问题

比如在青蛙跳台阶问题中：

$f(n - 1)$ 和 $f(n - 2)$ 称为 $f(n)$ 的最优子结构

$f(n) = f(n-1) + f(n-2)$ 被称为状态转移方程

$f(1) = 1, f(0) = 1$ 是边界。

$f(10) = f(9) + f(8), f(9) = f(8) + f(7)$ 就是重叠子问题

在动态规划中，我们只需要三个变量来存储就可以解决青蛙跳台阶问题了。

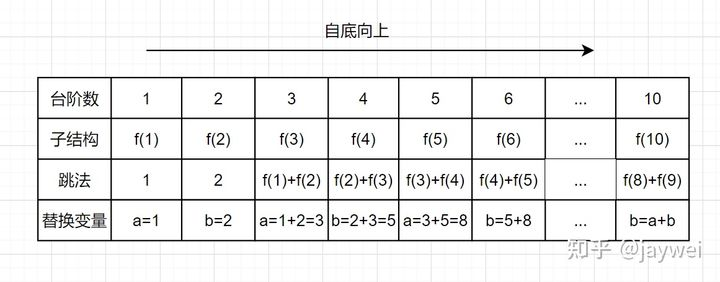
代码如下

public class Solution {
    public int runWays(int n) {
        if (n <= 1) {
            return 1;
        } else if (n == 2) {
            return 2;
        } else {
            int a = 1;
            int b = 2;
            int temp = 0;
            for (int i = 3; i <= n; i++) {
                temp = (a + b) % 1000000007;
                a = b;
                b = temp;
            }
            
            return temp;
        }
    }
}

动态规划的解题套路

什么样的问题可以考虑使用动态规划解决呢？

如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。

比如一些求最值的场景，如最长递增子序列、最小编辑问题、背包问题、凑零钱问题等等，都是动态规划的经典应用场景

动态规划的解题思路

动态规划的核心思想就是拆分子问题，记住过往，减少重复计算。并且动态规划一般都是自底向上的。

Reference

某天在网上看到的文章