ZY in NJU HomeArchivesTagsCategoriesAbout
Specific Tree
|软件工程数据结构与算法
字数总计: 2.8k|阅读时长: 10 分钟

Binary Search Tree 二叉搜索树

Definition(Binary Search Tree)

​ 二叉搜索树可以是一棵空树，如果它是非空的树，那么其满足以下的条件：

  1. 所有的节点都有一个值（key），且任意两个不同的节点的值是不同的。

    即所有的值都是唯一的

  2. 某节点的左子树的所有节点的值都小于该节点的值

  3. 某节点的右子树的所有节点的值都大于该节点的值

  4. 根节点的左子树和右子树都是二叉搜索树（递归）

带索引的二叉搜索树

即除了 左儿子，右儿子，值 之外，还加入一个索引leftSize，用于记录该节点的左子树的节点数量 + 1

二叉搜索树的增删改查

查找

与当前节点不断比较，如果比当前节点的值小，则递归到该节点的左子树，如果比当前节点的值大，则递归到该节点的右子树，如果相同则返回当前节点。

private BinaryNode find(Comparable x, BinaryNode t) {
    if (t == null) {
        return null;
    }
    
    if (x.compareTo(t.element) < 0) {
        // 值比当前节点小，递归到左子树
        return find(x, t.left)
    } else if (x.compareTo(t.element) > 0) {
        // 值比当前节点大，递归到右子树
        return find(t, x.right);
    } else {
        // 相等的时候直接返回当前节点
        return t;
    }
}

时间复杂度：O(H)O(H)，HH 为二叉搜索树的高度

findMax() 和 findMin()

找到该二叉搜索树的最小值和最大值

  1. 最小值即不断朝左子树走到尽头即可
  2. 最大值即不断朝右子树走到尽头即可

findMin() 递归算法

private BinaryNode findMin(BinaryNode t) {
    if (t == null) {
        return null;
    } else if (t.left == null) {
        return t;
    }
    
    return findMin(t.left);
}

findMax() 非递归算法

private BinaryNode findMax(BinaryNode t) {
    if (t != null) {
        while (t.right != null) {
            t = t.right;
        }
    }
    
    return t;
}

时间复杂度：O(H)O(H)，HH 为二叉搜索树的高度

插入

首先如果在树中找到了这个值，就不用插入了（值唯一）

与查找算法的思路类似，如果比当前节点大就往右子树走，比当前节点小就往左子树走，直到走的节点为空，那么就插入到该地方

private BinaryNode insert(Comparable, BinaryNode t) {
    // root : t
    if (t == null) {
        // 空树，该节点直接作为树根
        t = new BinaryNode(x, null, null);
    } else if (x.compareTo(t.element) < 0) {
        t.left = insert(x, t.left);
    } else if (x.compareTo(t.element) > 0) {
        t.right = insert(x, t.right);
    } else {
        // nothing to do
        // 相等说明该节点已经在二叉搜索树中，不需要插入
    }
    
    return t;
}

删除

对要删的节点 pp，有三种情况：

  1. pp 是树叶
  2. pp 有两棵非空子树
  3. pp 有一棵非空子树
private BinaryNode remove(Comparable x, BinaryNode t) {
    if (t == null) {
        return t;
    }
    
    if (t.compareTo(t.element) < 0) {
        t.left = remove(x, t.left);
    } else if (x.compareTo(t.element) > 0) {
        t.right = remove(x, t.right);
    } else {
        if (t.left != null && t.right != null) {
        	// 该节点存在两棵子树
        	// 转换成删左子树的最大节点或者右子树的最小节点的问题
            // 这里是将右子树的最小节点的值替换掉我们要删除的值，然后将原本右子树中最小的值的节点删除即可
        	t.element = findMin(t.right).element;
        	t.right = remove(t.element, t.right);
    	} else {
        	t = (t.left != null) ? t.left : t.right;
    	}
    }
    
    return t;
}

时间复杂度：O(H)O(H)，HH 为二叉搜索树的高度

二叉搜索树的高度

nn 个节点的二叉搜索树，情况最好的情况下是一棵完全二叉树，树的高度为 log⁡2(n)\log_2(n)，最坏的情况是直接变成了一条线

AVL Tree(自平衡的二叉搜索树)

目的：为了降低二叉搜索树的高度，降低时间复杂度

Definition(AVL Tree)

  1. AVL Tree是一棵二叉搜索树

  2. 所有节点满足：

可做可不做，做了可以加速某些算法的速度

Balance factor = 右子树高度 - 左子树高度（−1,0,1-1, 0, 1 三种情况）

nn 个节点的 AVL Tree的高度为 O(log⁡2(n))O(\log_2(n))，查询算法相同，时间复杂度相同。

AVL的插入

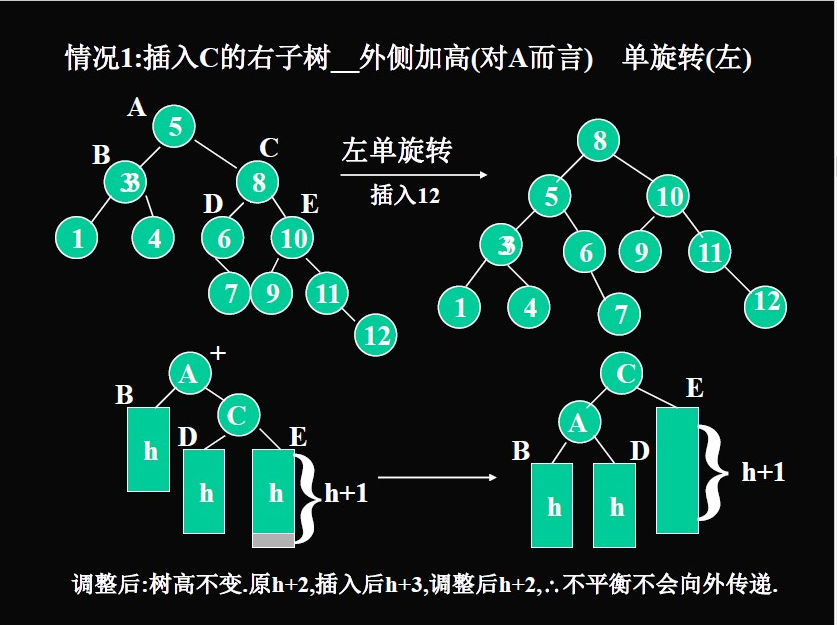
如果插入到高度较高的子树，就旋转。

  1. 插入到外侧的情况：单旋转。子树与树根互换，其余子树按顺序排列

  1. 插入到内侧的情况：双旋转。

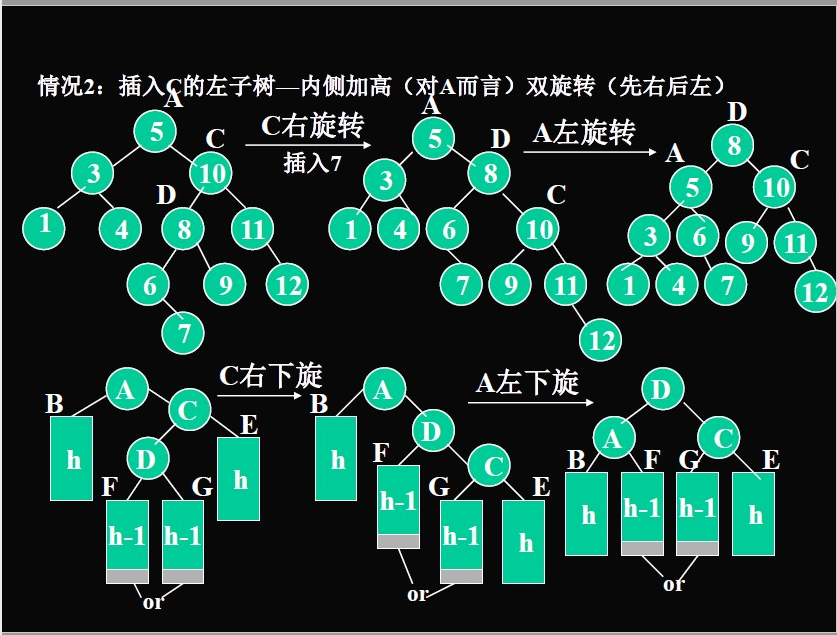
**注意：**调整之后，树的高度不变，调整不会影响到以A为根的子树以外的节点。

**如何调整：**回溯，通过不断判断某个子树的结构是不是符合AVL，如果符合就回到其父节点判断一棵更大的子树是不是符合。

或者这么说：插入一个新节点后，需要从插入位置沿通向根的路径回溯，检查各节点左右子树的高度差，如果发现某点高度不平衡则停止回溯。

注意分清外侧和内侧：只需要看两层，即是该节点的左子树的左子树（外侧），还是该节点的左子树的右子树（内侧）。还是该节点的右子树的左子树（内侧），或者是该节点的右子树的右子树（外侧）。以及注意当前检查节点的选择（回溯的节点）

时间复杂度：O(1)O(1)

Code

public class AVLTree {
    
    private class AVLNode {
        
        public AVLNode(Comparable theElement) {
            this(theElement, null, null);
        }
        
        public AVLNode(Comparable theElement, AVLNode lt, AVLNode, rt) {
            element = theElement;
            left = lt;
            right = rt;
            height = 0;
        }
        
        Comparable element;
        AVLNode left;
        AVLNode right;
        int height;
    }
    
    private static int height(AVLNode t) {
        // 判断是不是空树
        return t == null ? -1 : t.height;
    }
    
    private AVLNode insert(Comparable x, AVLNode t) {
        if (t == null) {
            t = new AVLNode(x, null, null);
        } else if (x.compareTo(t.element) < 0) {
            // 此时在左子树上
            t.left = insert(x, t.left);
            if (height(t.left) - height(t.right) == 2) {
                // 此时需要单旋
                t = rotateWithLeftChild(t);
            } else {
                // 否则需要双旋
                t = doubleWithLeftChild(t);
            }
        } else if (x.compareTo(t.element) > 0) {
            // 此时在右子树上
            t.right = insert(x, t.right);
            if (height(t.right) - height(t.left) == 2) {
                // 此时需要单旋
                t = rotateWithRightChild(t);
            } else {
                // 否则需要双旋
                t = doubleWithRightChild(t);
            }
        }
        
        // 更新高度
        t.height = Math.max(height(t.left), height(t.right)) + 1'
            
        return t;
    }
    
    private static AVLNode rotateWithLeftChild(AVLNode k2) {
        // k2是要旋转的节点的根节点
        // k1是k2的左子树，此时变为根节点。
        AVLNode k1 = k2.left;
        k2.left = k1.right;
        k1.right = k2;
        
        // 更新高度
        k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
        k1.height = Math.max(height(k1.left), k2.height) + 1;
        
        return k1;
    }
    
    private static AVLNode doubleWithLeftChild(AVLNode k3) {
        k3.left = rotateWithRightChild(k3.left);
        return rotateWithLeftChild(k3);
        
        // 右子树的旋转是对称的
    }
}

AVL树的删除

AVL树的删除和二叉搜索树的删除是相同的，只是在删除之后需要调整高度，调整高度的方法也是和上面的插入。

B-Trees

m-路搜索树

Definition

mm - 路搜索树可能是一颗空树，如果它不为空的话，那么它是一棵满足以下性质的树：

  1. 二叉搜索树扩展而来扩展搜索树（通过将外节点替换为空指针得到）。每个内部节点都最多有 mm 个子节点和 [1,m−1][1, m-1] 个元素（被称为关键码）

  2. 每个有 pp 个元素的节点都有 p+1p+1 个子节点

  3. 对任意有 pp 个关键码的节点来说：

​

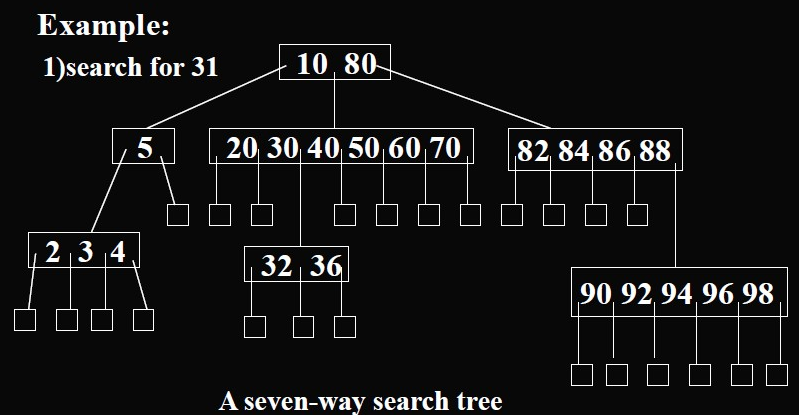
mm 路搜索树的节点个数（最多）：

mh−1m−1=m0+m1+⋯+mh−1\frac{m^h - 1}{m - 1} = m^0 + m^1 + \dots + m^{h-1}

因为每个节点最多有 m−1m - 1 个关键码，则关键码个数最多有 mh−1m^h - 1 个。

  1. mm - 路搜索树如果高度为 hh，那么它的关键码个数在 hh 到 mh−1m^h - 1 之间

  2. mm - 路搜索树如果有 nn 个节点，那么它的高度在 log⁡m(n+1)\log_m(n+1) 和 nn 之间

B树

B树是一棵高度平衡的 mm-路搜索树

  • 二叉搜索树 →\rightarrow 平衡的二叉搜索树（AVL树）
  • mm 路搜索树 →\rightarrow 平衡的 mm 叉搜索树（B-树）

Definition

  1. 树根至少要有两个子女（即关键码至少要有一个）
  2. 所有内节点（除了树根）至少要有 ⌈m2⌉\left \lceil \frac{m}{2}\right \rceil个节点
  3. 所有外节点都在同一层（level）

特殊的B树

  1. 二阶B树是一棵满二叉树
  2. 三阶B树，每个节点有1或2个关键码

性质

  1. 所有外节点都在同一层

  2. 外节点的数量 = 所有节点的关键码的数量 + 1

    1. kik_i：第 ii 层的节点数量
    2. bib_i：

    external\ node\ number = k_{h-1} + k_{h-2} + \dots + k_0 + 1 = n+ 1

B树的查找

相似于 mm 路搜索树的查询算法

实际运用场景：BB 树不一定会放在内存中，有可能会放在磁盘（外存）上。每次从磁盘上载入 BB 树的一个节点。（访问磁盘比遍历节点数据的时间还要长很多）

Q:Q: mm 阶 BB 树的一次查询，访问磁盘次数最多有 hh 次（hh 为B树的树高）

B树的插入

  1. 叶节点的关键码个数 <m−1< m-1，则直接插入到该叶节点的关键码的对应位置即可
  2. 叶节点的关键码个数 =m−1= m - 1（已经满了），此时要将该节点分裂成两个节点，并将中间节点拉到父节点

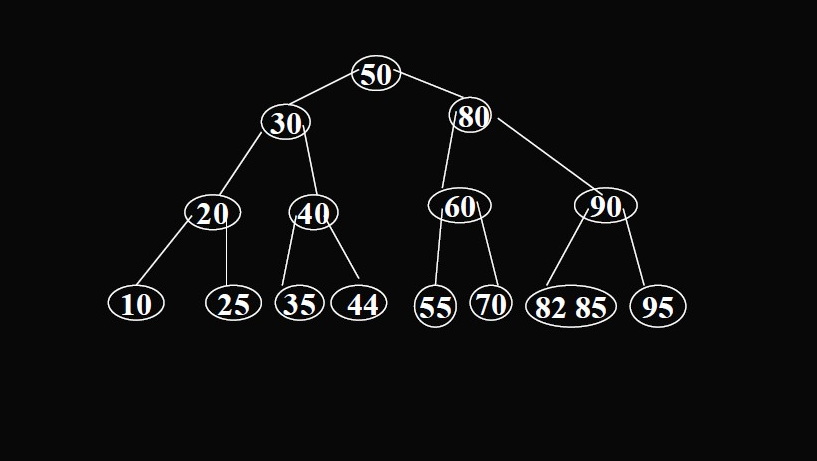
插入操作：最多访问：h+2s+1h + 2s + 1 次磁盘（hh 为树高， ss 次为分裂次数，其中 s≤hs \le h）

  1. hh：查询的时候从磁盘读取节点
  2. 2s2s：将分裂成两部分的节点写回到磁盘
  3. 11：写回新的节点（分裂到尽头有两种可能性：
    1. 如果树根也分裂了，那么会形成一个新的树根，该节点也需要写回到磁盘
    2. 如果树根没有分裂，那么最顶部的节点会插入一个关键码，也要写回到磁盘中

B树的删除

Cases（leaf）：

  1. 删除的关键码所在的节点的关键码个数很多，可以直接删除
  2. 删除后该节点的关键码的个数 <⌈m2⌉< \left \lceil \frac{m}{2} \right \rceil ，那么首先考虑从邻居借

如何从邻居借？

  1. 将左邻居的最大值拉到父节点，然后将对应的父节点的值拉到该节点
  2. 将右邻居的最小值拉到父节点，然后将对应的父节点的值拉到该节点

记得要将邻居被拉到父节点的关键码旁边的指针拉到空出来的节点

如果邻居节点也不够怎么办？

将两个节点做合并（树叶节点），然后将父节点对应的两个子节点所在指针中间的关键码拉下来，形成新的节点。

中间节点的删除

B树里关键码和指针的保存方法

线性表

文章作者: ZY
文章链接: https://zyinnju.com/2022/02/18/Specific-Tree/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZY in NJU！
Software EngineeringComputer ScienceData Structure